Teorema di Millman -

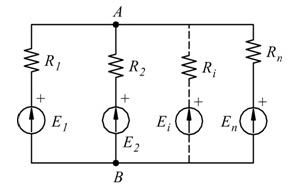
Viene applicato a circuiti costituiti da n rami in parallelo.
Ipotizzando che A e B siano i morsetti in comune fra gli n rami:

La tensione $V_{AB}$ risulta uguale alla corrente che si ottiene mettendo in corto circuito i morsetti A e B; essa è data da:

$\sum_{i=1}^{n} \frac{E_i}{R_i}$

moltiplicata per la resistenza $R_{AB}$ vista fra i morsetti in questione:

$R_{AB} = \frac{1}{\sum_{i=1}^{n} \frac{1}{R_i}}$

La sommatoria:

$\sum_{i=1}^{n} \frac{E_i}{R_i}$

è algebrica, cioè la f.e.m. $E_i$ che agisce sul ramo $i$ è positiva se ha il morsetto + rivolto verso il nodo A, negativa in caso contrario.

In definitiva risulterà essere:

$V_{AB} = \frac{ \sum_{i=1}^{n} \frac{E_i}{R_i} }{ \sum_{i=1}^{n} \frac{1}{R_i} }$

Teorema di Millman