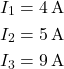Esercizo 9: Soluzione

Determinazione delle correnti in un circuito con due generatori

Utilizzando le leggi di Kirchhoff, si vuole determinare il valore delle tre correnti $I_1, I_2, I_3$ nel seguente circuito:

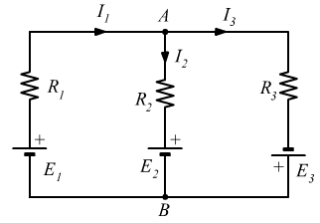
Si hanno i seguenti dati:

$\begin{aligned} &E_1= 12\,\text{V} \\ &E_2 = 6\,\text{V} \\ &R_1 = 2\,\Omega \\ &R_2 = 4\,\Omega \\ &R_3 = 6\,\Omega \\ \end{aligned}$

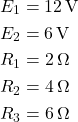
Assumiamo come convenzione che tutte le correnti siano positive se uscenti dal nodo. Applichiamo ora le leggi di Kirchhoff.

Legge di Kirchhoff ai nodi

Nel nodo in alto:

$I_1 = I_2 + I_3$

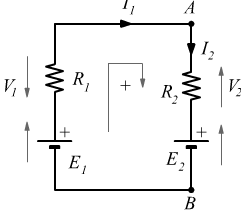
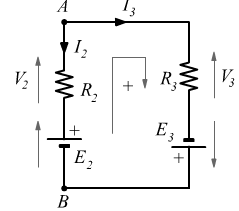
Applicazione delle leggi di Kirchhoff a un circuito a 3 maglie

Analizziamo le equazioni relative alle due maglie e alle correnti nel seguente circuito:

Legge di Kirchhoff alla maglia sinistra

$\begin{aligned} &0 = E_1 - V_1 - V_2 - E_2 \\ &E_1 - E_2 = V_1 + V_2 \\ &E_1 - E_2 = R_1 I_1 + R_2 I_2 \end{aligned}$

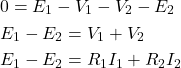
Legge di Kirchhoff alla maglia destra

$\begin{aligned} &0 = E_2 + V_2 - V_3 + E_3 \\ &E_2 + E_3 = V_3 - V_2 \\ &E_2 + E_3 = R_3 I_3 - R_2 I_2 \end{aligned}$

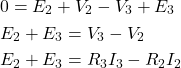
Legge di Kirchhoff al nodo

$I_1 = I_2 + I_3$

Equazioni ricavate

$\begin{cases}I_1 = I_2 + I_3 \\ E_1 - E_2 = R_1 I_1 + R_2 I_2 \\ E_2 + E_3 = R_3 I_3 - R_2 I_2 \\ \end{cases}$

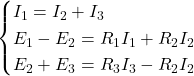
Sostituendo 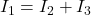$I_1 = I_2 + I_3$

$\begin{cases} E_1 - E_2 = R_1 (I_2 + I_3) + R_2 I_2 \\ E_2 + E_3 = R_3 I_3 - R_2 I_2 \end{cases}$

Espressione finale delle equazioni

$\begin{cases} E_1 - E_2 = R_1 I_2 + R_1 I_3 + R_2 I_2 \\ E_2 + E_3 = R_3 I_3 - R_2 I_2 \end{cases}$

Sostituendo i valori numerici

$\begin{cases} 10 - 7 = 2 I_2 + 2 I_3 + I_2 \\ 7 + 7 = 3 I_3 - I_2 \end{cases}$

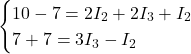
Forma finale del sistema

$\begin{cases} 3 = 2 I_2 + 3 I_3 \\ 14 = I_3 - I_2 \end{cases}$

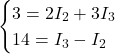
Risoluzione finale del sistema

Dunque:

$\begin{cases} 3 = 2(14 + I_2) + 3 I_2 \\ I_3 = 14 + I_2 \end{cases}$

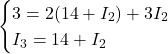
Proseguendo sulla prima equazione:

$\begin{cases} 3 = 28 + 2 I_2 + 3 I_2 \\ I_3 = 14 + I_2 \end{cases}$

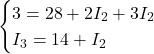
Da cui:

$3 - 28 = 5 I_2 \Rightarrow I_2 = \frac{-25}{5} = -5\,\text{A}$

Quindi la corrente $I_2$ vale 5 A ma ha verso contrario a quello inizialmente ipotizzato.

$\begin{aligned} I_3 &= 14 + (-5) = 9\,\text{A} \\ I_1 &= I_2 + I_3 = -5 + 9 = 4\,\text{A} \end{aligned}$

Valori finali correnti circuito Kirchhoff

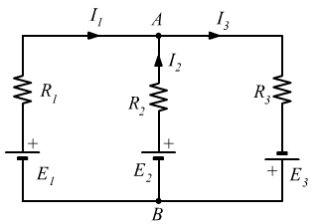
L’effettivo verso delle correnti nel circuito sarà quello indicato in figura. Il loro valore sarà:

$\begin{aligned} I_1 &= 4\,\text{A} \\ I_2 &= 5\,\text{A} \\ I_3 &= 9\,\text{A} \end{aligned}$