Esercizio 4: Soluzione -

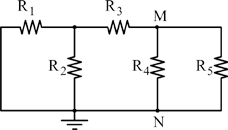
Riaggiustando (un minimo) il circuito, possiamo rappresentarlo così:

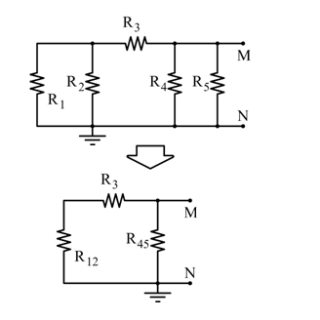
Calcolo delle resistenze equivalenti

1. Parallelo tra R₁ e R₂:

$R_{12} = \frac{R_1 R_2}{R_1 + R_2} = \frac{1{,}2 \cdot 3}{4{,}2} = 0{,}857\,\text{k}\Omega$

2. Parallelo tra R₄ e R₅:

$R_{45} = \frac{R_4 R_5}{R_4 + R_5} = \frac{2 \cdot 85}{87} = 1{,}954\,\text{k}\Omega$

3. Serie tra R₁₂ e R₃:

$R_{123} = R_{12} + R_3 = 0{,}873 + 0{,}170 = 1{,}043\,\text{k}\Omega$

Resistenza equivalente tra M e N

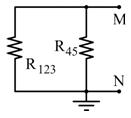
$R_{MN} = \frac{R_{123} \cdot R_{45}}{R_{123} + R_{45}} = \frac{1{,}043 \cdot 1{,}954}{1{,}043 + 1{,}954}$

$R_{MN} \approx 0{,}68\,\text{k}\Omega = 680\,\Omega$

Conclusione
La resistenza equivalente tra i punti M e N è:

$\boxed{R_{MN} = 680\,\Omega}$

Esercizio 4: Soluzione