Esercizio 3: Soluzione

DiAlfredo Di Fiore

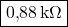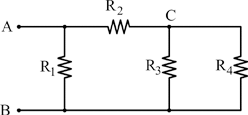
In questo esercizio analizziamo un circuito composto da quattro resistori collegati in una configurazione mista. L’obiettivo è calcolare la resistenza equivalente tra due coppie di punti:

  • tra i punti A e B
  • tra i punti A e C

Resistenza tra A e B
La configurazione iniziale può essere sintetizzata graficamente nel seguente modo:

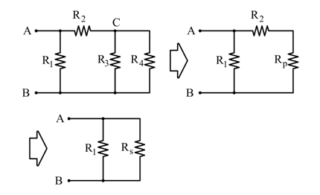
Calcoli

Cominciamo calcolando la resistenza equivalente tra R₃ e R₄ in parallelo:

R_P = \frac{R_3 R_4}{R_3 + R_4} = \frac{22 \cdot 0{,}4}{22 + 0{,}4} = 0{,}392\,\text{k}\Omega

Somma in serie di R₂ e RP:

R_S = R_2 + R_P = 1{,}2 + 0{,}392 = 1{,}592\,\text{k}\Omega

Parallelo tra R₁ e RS:

R_{AB} = \frac{R_1 R_S}{R_1 + R_S} = \frac{3 \cdot 1{,}592}{3 + 1{,}592} = 1{,}040\,\text{k}\Omega

R_P = \frac{R_3 R_4}{R_3 + R_4} = \frac{22 \cdot 0{,}4}{22 + 0{,}4} = 0{,}392\,\text{k}\Omega

Quindi calcoliamo la somma in serie tra R₂ e RP:

R_S = R_2 + R_P = 1{,}2 + 0{,}392 = 1{,}592\,\text{k}\Omega

Infine, troviamo la resistenza equivalente tra A e B:

R_{AB} = \frac{R_1 R_S}{R_1 + R_S} = \frac{3 \cdot 1{,}592}{3 + 1{,}592} = 1{,}040\,\text{k}\Omega

R_P = \frac{R_3 R_4}{R_3 + R_4} = \frac{22 \cdot 0{,}4}{22 + 0{,}4} = 0{,}392\,\text{k}\Omega

Resistenza tra A e C
Il circuito viene rielaborato così per l’analisi tra A e C:

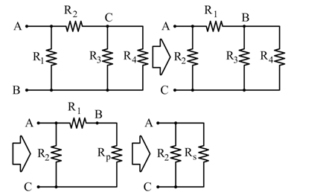
Calcoli
La resistenza RP è la stessa del caso precedente:

R_P = \frac{R_3 R_4}{R_3 + R_4} = 0{,}392\,\text{k}\Omega

Somma R₁ + RP:

R_S = R_1 + R_P = 3 + 0{,}392 = 3{,}392\,\text{k}\Omega

Resistenza equivalente tra A e C:

R_{AC} = \frac{R_2 \cdot R_S}{R_2 + R_S} = \frac{1{,}2 \cdot 3{,}392}{1{,}2 + 3{,}392} = 0{,}88\,\text{k}\Omega

R_P = \frac{R_3 R_4}{R_3 + R_4} = 0{,}392\,\text{k}\Omega

Sommiamo R₁ + RP per ottenere RS:

R_S = R_1 + R_P = 3 + 0{,}392 = 3{,}392\,\text{k}\Omega

Ora possiamo calcolare la resistenza equivalente tra A e C:

R_{AC} = \frac{R_2 \cdot R_S}{R_2 + R_S} = \frac{1{,}2 \cdot 3{,}392}{1{,}2 + 3{,}392} = 0{,}88\,\text{k}\Omega

Conclusioni

  • Resistenza equivalente tra A e B: \boxed{1{,}040\,\text{k}\Omega}
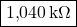
  • Resistenza equivalente tra A e C: \boxed{0{,}88\,\text{k}\Omega}

Articoli simili