Esercizio 13: Soluzione

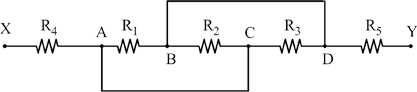
Notiamo come, a causa dei cortocircuiti, alcuni nodi coincidano e siano sovrapponibili: A = C e B = D. È immediato osservare come le resistenze R₁ e R₂ siano in parallelo.

Figura 1 – Schema iniziale e riconoscimento dei nodi

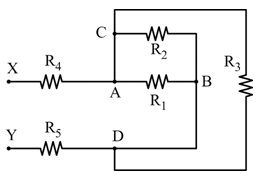
Essendo in parallelo, calcoliamo la resistenza equivalente:

$R_{12} = R_1 \parallel R_2 = \frac{2 \cdot 1}{2 + 1} = \frac{2}{3}\,\text{k}\Omega$

Il circuito può essere ridisegnato così, con R₁₂ e R₃ in parallelo.

Figura 2 – Nuovo schema con R₁₂ e R₃

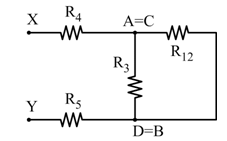
Ora calcoliamo:

$R_{123} = R_3 \parallel R_{12} = \frac{3 \cdot \frac{2}{3}}{3 + \frac{2}{3}} = \frac{2}{\frac{11}{3}} = \frac{6}{11}\,\text{k}\Omega$

Infine, sommiamo in serie con R₄ e R₅:

Figura 3 – Schema finale e calcolo di R_XY

$R_{XY} = R_4 + R_{123} + R_5 = 0{,}4 + \frac{6}{11} + 0{,}5 = 1{,}445\,\text{k}\Omega$

✅ Risultato finale: $R_{XY} = 1{,}445\,\text{k}\Omega$

Osservazioni didattiche

Questo esercizio è perfetto per approfondire i casi in cui cortocircuiti modificano la topologia del circuito. L’analisi nodo per nodo consente di ridurre efficacemente lo schema in elementi equivalenti.

Osservazioni didattiche

Articoli correlati

Test