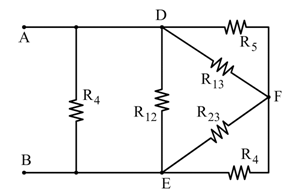
La stella di resistenze R1, R2, R3 può essere ricondotta ad un triangolo equivalente utilizzando le seguenti formule:
![]()
![]()
![]()
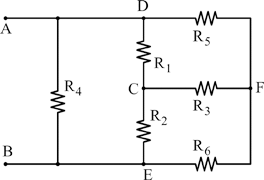
Figura 1 – Schema del circuito e trasformazione stella-triangolo
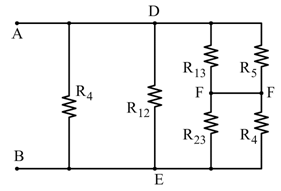
Dato che ![]() , tutte le nuove resistenze del triangolo risultano uguali:
, tutte le nuove resistenze del triangolo risultano uguali:
![]()
Ora calcoliamo la resistenza equivalente tra R5 e R13 in parallelo:
![]()
Essendo in serie, la loro somma è:
![]()
Ora possiamo calcolare la resistenza totale tra i punti A e B:
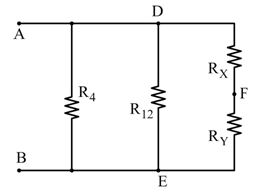
![]()
Risultato finale:
![]()
Considerazioni
Questa esercitazione mostra chiaramente come la trasformazione stella-triangolo e l’analisi dei collegamenti serie/parallelo permettano di risolvere circuiti complessi con semplicità ed eleganza.