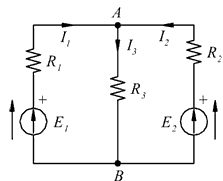
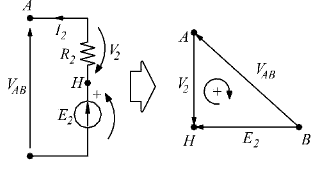
Applicando la formula:
\( V_{AB} = \frac{ \sum_{i=1}^{n} \frac{E_i}{R_i} }{ \sum_{i=1}^{n} \frac{1}{R_i} } \)avremo:
\( V_{AB} = \frac{ \frac{11}{2} + \frac{7}{1} + \frac{1}{2} }{ \frac{1}{2} + \frac{1}{1} + \frac{1}{2} } = \frac{11+14+1}{2+2} = \frac{26}{4} = \frac{13}{2} = 6,5\ \mathrm{V} \)Ai capi della resistenza \(R_3\) possiamo applicare la legge di Ohm: dato che \(V_{AB} = R_3 \cdot I_3\), avremo:
\( I_3 = \frac{V_{AB}}{R_3} = \frac{5}{1} = 5\ \mathrm{A} \)Studiamo ora il ramo della \(R_1\) applicando Kirchhoff:
\(I_1\) è negativa, quindi il suo valore è \(3 A\) ma il verso è contrario a quello ipotizzato nel primo disegno.
Studiamo ora il ramo della \(R_2\) applicando Kirchhoff:
