Esercizio 9: Soluzione

Forza elettrostatica e lavoro in un condensatore piano

Un condensatore costituito da due armature piane parallele, ha come dielettrico l’aria. Esso, dopo esser stato caricato alla tensione \( V = 360 \, \text{V} \) viene sottoposto a delle forze che allontanano fra loro le armature (che restano parallele) di \( 0{,}6 \, \text{mm} \).
Calcola il valore della forza elettrostatica che sollecita ciascuna armatura ed il lavoro compiuto per allontanare le due armature. Le dimensioni del condensatore sono
\( S = 84{,}6 \, \text{cm}^2 \) e \( d = 1{,}8 \, \text{mm} \).

Soluzione

1) Calcolo della carica 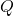\( Q \)

Q = C \cdot V = \varepsilon_0 \cdot \frac{S}{d} \cdot V = 8{,}86 \cdot 10^{-12} \cdot \frac{84{,}6 \cdot 10^{-4}}{1{,}8 \cdot 10^{-3}} \cdot 360

Q = 15 \cdot 10^{-9} \, \text{C}

2) Calcolo della forza elettrostatica

La forza elettrostatica si calcola con:

F = \frac{1}{2} \varepsilon \cdot \frac{S}{d^2} V^2 = \frac{1}{2} \cdot \frac{Q^2}{\varepsilon \cdot S} = \frac{1}{2} \cdot \frac{Q \cdot V}{d}

Dato che la carica \( Q \) resta costante, possiamo usare:

F = \frac{1}{2} \cdot \frac{Q^2}{\varepsilon_0 \cdot S} = \frac{15^2 \cdot 10^{-18}}{2 \cdot 8{,}86 \cdot 10^{-12} \cdot 84{,}6 \cdot 10^{-4}}

F = 1{,}5 \cdot 10^{-3} \, \text{N}

3) Calcolo del lavoro compiuto

Il lavoro per spostare le armature di \delta = 0{,}6 \, \text{mm} è:

L = F \cdot \delta = 1{,}5 \cdot 10^{-3} \cdot 0{,}6 \cdot 10^{-3} = 0{,}9 \cdot 10^{-6} \, \text{J}

Articoli correlati

Esercizio 20: Soluzione

Esercizio 19: Soluzione

Esercizio 18: Soluzione