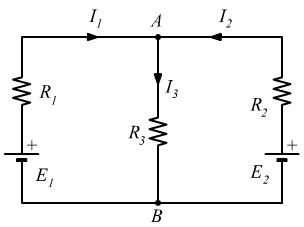
Esercizio 8 – Soluzione
Dati noti
Legge di Kirchhoff al nodo A
![]()
Equazione della maglia sinistra
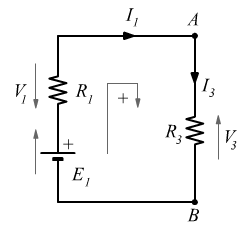
![]()
Equazione della maglia destra
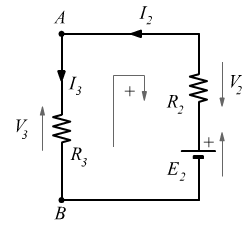
![]()
Inseriamo i valori
Risoluzione di un circuito elettrico con le leggi di Kirchhoff
Consideriamo un circuito composto da tre resistori \( R_1 = 1\,\Omega \), \( R_2 = 2\,\Omega \), \( R_3 = 3\,\Omega \) e due generatori di tensione \( E_1 = 11\,\text{V} \) e \( E_2 = 7\,\text{V} \). Applichiamo le leggi di Kirchhoff per determinare le correnti nei rami.
![Rendered by QuickLaTeX.com \begin{aligned} &\textbf{Equazioni iniziali:} \\ &\begin{cases} I_3 = I_1 + I_2 \\ E_1 = R_1 I_1 + R_3 I_3 \\ E_2 = R_3 I_3 + R_2 I_2 \end{cases} \\[10pt] &\textbf{Inserendo i valori:} \\ &\begin{cases} E_1 = 1 \cdot I_1 + 3 \cdot I_3 = I_1 + 3 I_3 \\ E_2 = 3 \cdot I_3 + 2 \cdot I_2 = 3 I_3 + 2 I_2 \\ I_3 = I_1 + I_2 \end{cases} \\[10pt] &\textbf{Sostituendo } I_1 = I_3 - I_2 \text{ nella prima equazione:} \\ &11 = (I_3 - I_2) + 3 I_3 = 4 I_3 - I_2 \\[10pt] &\textbf{Dalla seconda equazione:} \\ &7 = I_3 + I_2 \Rightarrow I_3 = 7 - I_2 \\[10pt] &\textbf{Sostituendo in } 11 = 3 I_3 - 2 I_2: \\ &11 = 3(7 - I_2) - 2 I_2 = 21 - 3 I_2 - 2 I_2 = 21 - 5 I_2 \\ &\Rightarrow 5 I_2 = 10 \Rightarrow I_2 = \frac{10}{5} = 2\,\mathrm{A} \\[10pt] &\textbf{Calcolando gli altri valori:} \\ &I_3 = 7 - I_2 = 7 - 2 = 5\,\mathrm{A} \\ &I_1 = I_3 - I_2 = 5 - 2 = 3\,\mathrm{A} \end{aligned}](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-3847c23563f19339d51b780857d66a52_l3.png)
Abbiamo quindi determinato le correnti nei tre rami del circuito:
- Corrente I1: 3 A
- Corrente I2: 2 A
- Corrente I3: 5 A
La soluzione è coerente con le leggi di Kirchhoff e verifica la corretta distribuzione delle correnti nei nodi e nelle maglie.

![]()
Legge di Kirchhoff: 
![]()
Verifica
![]()