Dati
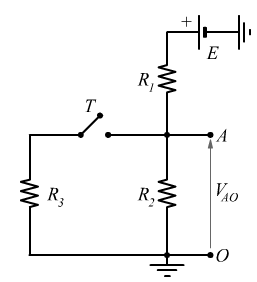
Situazione con tasto T aperto
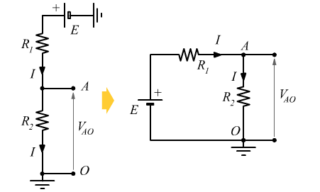
La corrente del generatore percorre solo ![]() . Applichiamo la legge di Ohm:
. Applichiamo la legge di Ohm:
![]()
![]()
Situazione con tasto T chiuso
Calcolo analitico di 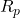 e
e 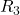
Per la regola del partitore di tensione:
![]()
![]()
![]()
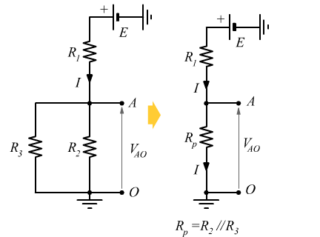
Espressione del parallelo 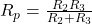
![]()
![]()
![]()
La tensione al punto A scende di 3 V, quindi:
![]()
Resistenza equivalente 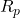 tra
tra 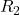 e
e 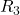
![]()
Applichiamo la formula del partitore di tensione:
![]()
Sostituiamo i dati:
![]()
![]()
![]()
Ricaviamo 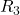 dalla formula del parallelo
dalla formula del parallelo
![]()
![]()
![]()
Metodo alternativo per calcolare 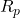
Poiché la resistenza ![]() è tra le due d.d.p.
è tra le due d.d.p. ![]() , possiamo scrivere:
, possiamo scrivere:
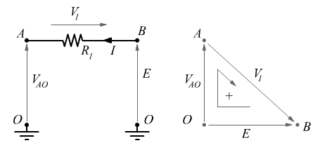
![]()
Ricaviamo la corrente ![]() :
:
![]()
Questa è la corrente che attraversa la resistenza ![]() . Allora, per la legge di Ohm:
. Allora, per la legge di Ohm:
![]()
Come già trovato nel metodo precedente.