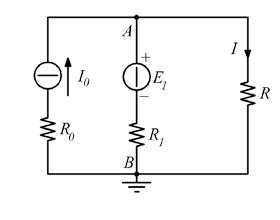
Nel ramo del generatore ![]() può scorrere solo la
può scorrere solo la ![]() .
.
Nel valutare le conduttanze nei singoli rami coi generatori di tensione cortocircuitati e i generatori di corrente aperti, la conduttanza vista sul ramo del generatore ![]() è nulla, dato che la resistenza di un circuito aperto è infinita.
è nulla, dato che la resistenza di un circuito aperto è infinita.
![]()
![]()
Verificando col teorema di Thevenin:

Per il calcolo della ![]() , bisogna dire che tolto il carico, l’unica corrente circolante è la
, bisogna dire che tolto il carico, l’unica corrente circolante è la ![]() .
.
![]()
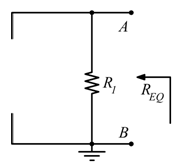
La resistenza equivalente vista ai morsetti AB col carico R staccato, col generatore di corrente aperto e col generatore di tensione cortocircuitato, vale ![]() .
.
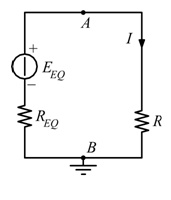
Riattaccando ai capi del carico il circuito equivalente Thevenin, la corrente ![]() che passa dentro la resistenza
che passa dentro la resistenza ![]() è:
è:
![]()
Come trovato col teorema di Millman.