![]()
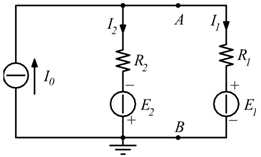
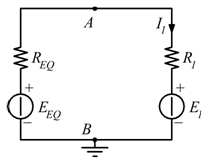
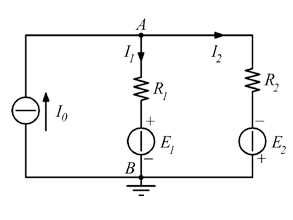
Eseguendo la legge di Kirchhoff al ramo di ![]() ed
ed ![]() :
:
![]()
![]()
Eseguendo la legge di Kirchhoff al ramo di ![]() ed
ed ![]() :
:
![]()
![]()
Eseguendo la prima legge di Kirchhoff al nodo A:
![]()
La I₀ risulta verificata.
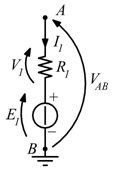
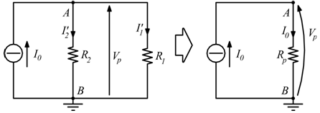
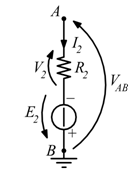
Verifico la ![]() col teorema di Thevenin; riscrivo il circuito (per comodità) e poi stacco il carico, in questo caso costituito dalla serie
col teorema di Thevenin; riscrivo il circuito (per comodità) e poi stacco il carico, in questo caso costituito dalla serie ![]() .
.
La Tensione a vuoto misurata ai capi dei morsetti AB diventerà il generatore equivalente.
In tali condizioni l’unica corrente che può percorrere la ![]() è la
è la ![]() stessa.
stessa.
![]()
![]()
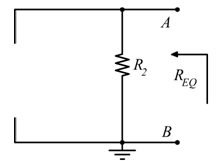
Per il calcolo della ![]() , dobbiamo cortocircuitare i generatori di tensione e aprire i generatori di corrente.
, dobbiamo cortocircuitare i generatori di tensione e aprire i generatori di corrente.
In tali condizioni dobbiamo valutare la resistenza che si vede ai capi dei morsetti AB. Quindi:
![]()
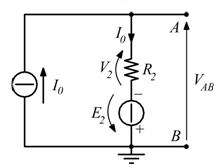
A questo punto, ai capi del circuito equivalente Thevenin, riagganciamo il carico precedentemente escluso.
L’unica corrente circolante è appunto la ![]() , data da:
, data da:
![]()
Come ottenuto col teorema di Millman.
Verifica della I₂ col principio di sovrapposizione degli effetti
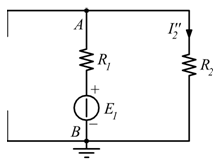
Nel primo caso faccio funzionare solo il generatore ![]() ; questa corrente viene convogliata nel parallelo
; questa corrente viene convogliata nel parallelo ![]() :
:
![]()
La tensione ![]() ai capi del parallelo sarà:
ai capi del parallelo sarà:
![]()
Quindi:
![]()
Nel secondo caso, facciamo funzionare solo il generatore ![]() ; in questo caso
; in questo caso ![]() è cortocircuitato ed il generatore di corrente
è cortocircuitato ed il generatore di corrente ![]() deve essere aperto.
deve essere aperto.
![]()
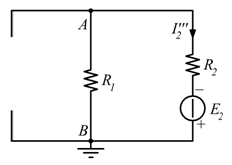
Nel terzo caso, facciamo funzionare solo il generatore ![]() ;
; ![]() in questo caso è cortocircuitato ed il generatore di corrente
in questo caso è cortocircuitato ed il generatore di corrente ![]() deve essere aperto.
deve essere aperto.
![]()
Tutte e tre le correnti parziali trovate hanno come verso di percorrenza lo stesso della ![]() indicato nel circuito originario.
indicato nel circuito originario.
Esse sono quindi da considerare tutte algebraicamente positive.
![]()
Come trovato col teorema di Millman.