Calcoliamo il valore di ![]() utilizzando la formula generale:
utilizzando la formula generale:
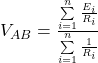
Sostituendo i valori forniti:
![]()
Quindi:
![]()
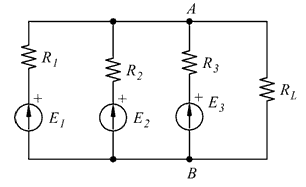
Ora possiamo calcolare la corrente ![]() attraverso la resistenza di carico
attraverso la resistenza di carico ![]() :
:
![]()
Quindi la corrente risulta:
![]()
Megistone - Per non perdere l'orientamento
Calcoliamo il valore di ![]() utilizzando la formula generale:
utilizzando la formula generale:
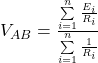
Sostituendo i valori forniti:
![]()
Quindi:
![]()
Ora possiamo calcolare la corrente ![]() attraverso la resistenza di carico
attraverso la resistenza di carico ![]() :
:
![]()
Quindi la corrente risulta:
![]()