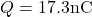Condensatore con piatti circolari: capacità e carica accumulata
Un condensatore piano ha piatti circolari di raggio:
![]()
posti a una distanza:
![]()
Problema
-
Calcolare la capacità del condensatore.
-
Determinare la carica accumulata quando si applica una differenza di potenziale di:
![]()
Soluzione
1. Calcolo della capacità
La formula per la capacità di un condensatore piano con piatti circolari è:
![]()
Sostituendo i valori:
![]()
Quindi:
![]()
2. Calcolo della carica accumulata
Dalla relazione:
![]()
Convertiamo in nanocoulomb:
![]()
Risultati finali
-
Capacità:
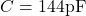
-
Carica accumulata: