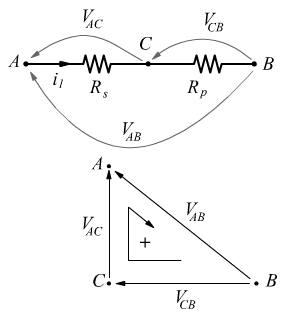
Analisi di un circuito con resistenze in serie e parallelo
In questo tratto di circuito sono note le seguenti informazioni:
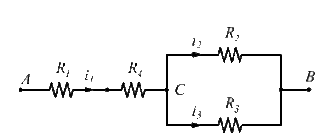
Le resistenze:
Si richiede di determinare:
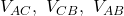
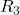
- La resistenza equivalente
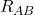
1. Calcolo delle tensioni
Dato che conosciamo le resistenze ![]() e la corrente
e la corrente ![]() , possiamo trovare la tensione
, possiamo trovare la tensione ![]() .
.
Il tratto AC comprende due resistenze in serie:
![]()
Applichiamo la legge di Ohm:
![]()
2) Calcolo di 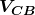 e corrente
e corrente 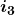
Il tratto ![]() è costituito da due resistenze in parallelo, percorse dalle correnti
è costituito da due resistenze in parallelo, percorse dalle correnti ![]() .
.
Applicando il 1° principio di Kirchhoff al nodo ![]() :
:
![]()
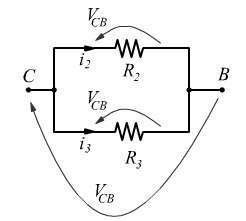
Dal disegno si nota che la tensione
![]()
In alternativa, la tensione si può esprimere come:
![]()
Ma in questo momento ![]() è sconosciuta.
è sconosciuta.
Somma delle tensioni e circuito equivalente
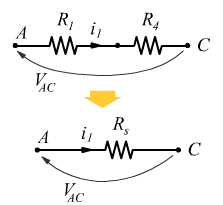
Una volta realizzata la serie fra ![]() e
e ![]() (denominata
(denominata ![]() e il parallelo fra
e il parallelo fra ![]() e
e ![]() (denominato
(denominato ![]() , il circuito assume la forma seguente:
, il circuito assume la forma seguente:
La tensione totale \( V_{AB} \) è la somma di \( V_{AC} \) e \( V_{CB} \):
![]()
Verifica con la legge delle maglie
Applichiamo il 2° principio di Kirchhoff alla maglia ABC (in senso orario):
![]()
3) Calcolo di 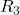
La tensione ai capi di una resistenza in parallelo è la stessa per entrambi i rami:
![]()
Resistenza equivalente tra i morsetti A-B
La formula equivalente è:
![]()
Sostituendo i valori:
![]()