Esercizio 13: Soluzione

DiAlfredo Di Fiore

Traiettoria di una particella carica in un condensatore piano

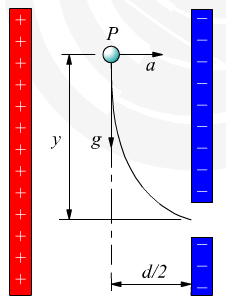
Una particella di carica \( Q = 1 \, \text{mC} \) e massa \( m = 1 \, \text{mg} \), inizialmente ferma, viene lasciata libera da un punto \( P \), posto a metà tra le facce di un condensatore piano mantenuto ad una differenza di potenziale costante \( V \), come nel disegno.
Altri dati sono \( d = 12 \, \text{cm} \) (distanza tra le armature) e \( V = 1 \, \text{V} \) (tensione a cui è caricato il condensatore).
A quale distanza in verticale \( y \) dal punto \( P \) deve essere praticato un foro sulla faccia del condensatore in modo che la particella ci passi attraverso?

Soluzione

1) Moto orizzontale

Forza orizzontale: F = Q E
Campo elettrico: E = \frac{V}{d} = \frac{1}{0{,}12} = 8{,}3 \, \frac{\text{V}}{\text{m}}
Accelerazione: a = \frac{Q E}{m} = \frac{10^{-3} \cdot 8{,}3}{10^{-6}} = 8{,}3 \cdot 10^3 \, \text{m/s}^2

2) Spostamento orizzontale e tempo

Dal disegno: x = \frac{d}{2} = \frac{12}{2} = 6 \, \text{cm} = 0{,}06 \, \text{m}

x = \frac{1}{2} a t^2 \quad \Rightarrow \quad t = \sqrt{\frac{2x}{a}} = \sqrt{\frac{2 \cdot 0{,}06}{8{,}3 \cdot 10^3}} = 0{,}12 \, \text{s}

3) Caduta verticale

y = \frac{1}{2} g t^2 = \frac{9{,}81 \cdot (0{,}12)^2}{2} = 0{,}07 \, \text{m} = 7 \, \text{cm}

Articoli simili