Esercizio 13

🧮 Esercizi sulle Disposizioni

🔹 Esercizio 13 – Parole di 4 lettere con condizioni specifiche

Domande:

• Quante parole di 4 lettere tutte diverse (senza ripetizioni) si possono formare con le 21 lettere dell’alfabeto italiano?
• Quante iniziano con una consonante?
• Quante iniziano con la sigla “TO”?
• Quante terminano con una vocale?

✅ Soluzioni:

• 1) Parole di 4 lettere tutte diverse:
  
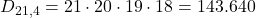
• 2) Parole che iniziano con una consonante:
  Le consonanti sono 16, quindi per ciascuna si possono combinare 3 lettere tra le rimanenti 20:
  
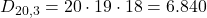
  Totale: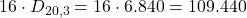
• 3) Parole che iniziano con “TO”:
  Le lettere “T” e “O” sono fissate, quindi restano 19 lettere per scegliere le altre due:
  
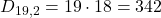
• 4) Parole che terminano con una vocale:
  Le vocali sono 5. Per ogni vocale che va alla fine, si scelgono 3 lettere tra le altre 20:
  
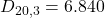
  Totale: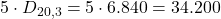

📌 Risultati finali:

• Parole di 4 lettere (tutte diverse): 143.640
• Iniziano con una consonante: 109.440
• Iniziano con “TO”: 342
• Terminano con una vocale: 34.200