Esercizio 11: Soluzione

Nel circuito assegnato si vuole determinare il valore della resistenza incognita $R_x$ , noti i seguenti dati:

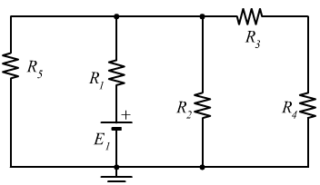
Dati del problema

${\small $ \begin{array}{ll} E_1 = 12\,\text{V} \\ R_1 = 1\,\Omega \\ R_2 = 1\,\Omega \\ R_3 = 3\,\Omega \\ R_5 = 2\,\Omega \\ I_1 = 2\,\text{A} \end{array} $ }$

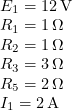
Soluzione:
Dalla prima maglia si può calcolare la tensione ai capi di $R_5$ :

$V_{AB} = R_5 I_1 = 3 \cdot 2 = 6\,\text{V}$

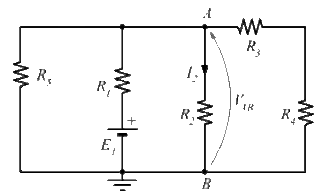
Si esegue una semplificazione del circuito con il generatore e le resistenze equivalenti.
Adesso $R_3$ è in parallelo a $R_4$ , e la loro combinazione è in serie con $R_2$ .

$R_{34} = R_3 + R_4$

Configurazione equivalente e risoluzione:

$\text{con } R_{34} = R_3 + R_4$
$\text{e con } \frac{1}{R_p} = \frac{1}{R_2} + \frac{1}{R_5} + \frac{1}{R_{34}}$
$\text{trattando di un partitore} \quad V_{AB} = \frac{E_T R_p}{R_1 + R_p} \quad \Rightarrow \quad 6 = \frac{12 R_p}{1 + R_p}$
$\text{quindi } 1 + R_p = 2 R_p \quad \Rightarrow \quad R_p = 1\,\Omega$
$\frac{1}{1} = \frac{1}{3} + \frac{1}{2} + \frac{1}{R_{34}} \quad \Rightarrow \quad \frac{1}{R_{34}} = 1 - \frac{1}{2} - \frac{1}{3}$
$\text{si ha } \frac{1}{R_{34}} = \frac{6 - 3 - 2}{6} = \frac{1}{6} \quad \Rightarrow \quad R_{34} = 6\,\Omega$
$\text{quindi } R_{34} = R_3 + R_4 \quad \Rightarrow \quad 6 = 4 + R_4 \quad \Rightarrow \quad \boxed{R_4 = 2\,\Omega}$

Dati del problema

Articoli correlati

Esercizio 12: Soluzione

Esercizio 10: Soluzione

Esercizo 9: Soluzione