Ven. Apr 25th, 2025

Esercizio 10: Soluzione

Determinazione delle tre correnti tramite le leggi di Kirchhoff

Utilizzando le leggi di Kirchhoff, si vogliono determinare le tre correnti \( I_1, I_2, I_3 \) nel circuito seguente:

Risoluzione circuito Kirchhoff con tre maglie

Dati del problema

$\begin{aligned} E_1 &= 4\,\text{V} \\ E_2 &= 11\,\text{V} \\ E_3 &= 12\,\text{V} \\ R_1 &= 1\,\Omega \\ R_2 &= 2\,\Omega \\ R_3 &= 3\,\Omega \end{aligned}$

Come si nota, le correnti sono già disposte secondo il loro senso più probabile, considerando che una corrente viene erogata sempre dal polo positivo del generatore.

Equazione al nodo A

$I_1 = I_2 + I_3$

Equazione alla maglia sinistra

Maglie Kirchhoff e nodi

$\begin{aligned} 0 &= V_1 + V_2 - E_2 - E_1 \\ E_1 + E_2 &= V_1 + V_2 \\ E_1 + E_2 &= R_1 I_1 + R_2 I_2 \end{aligned}$

Equazione alla maglia destra

$\begin{aligned} 0 &= E_2 - V_2 + V_3 - E_3 \\ E_3 - E_2 &= V_3 - V_2 \\ E_3 - E_2 &= R_3 I_3 - R_2 I_2 \end{aligned}$

Soluzione del sistema tramite le leggi di Kirchhoff

Si consideri il seguente sistema di equazioni:

$\begin{cases} I_1 = I_2 + I_3 \\ E_1 + E_2 = R_1 I_1 + R_2 I_2 \\ E_3 - E_2 = R_3 I_3 - R_2 I_2 \end{cases}$

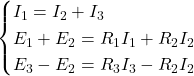
Espressione delle equazioni con sostituzione di \( I_1 \):

$\begin{cases} E_1 + E_2 = R_1 (I_2 + I_3) + R_2 I_2 \\ E_3 - E_2 = R_3 I_3 - R_2 I_2 \end{cases}$

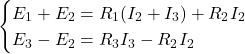
Sviluppando:

$\begin{cases} E_1 + E_2 = R_1 I_2 + R_1 I_3 + R_2 I_2 \\ E_3 - E_2 = R_3 I_3 - R_2 I_2 \end{cases}$

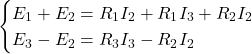
Fattorizzando la prima equazione:

$E_1 + E_2 = (R_1 + R_2) I_2 + R_1 I_3$

Sistema Kirchhoff risoluzione finale

Sostituendo i valori:

$\begin{cases} 4 + 11 = (1 + 2) I_2 + 1 \cdot I_3 \\ 12 - 11 = 3 I_3 - 2 I_2 \end{cases}$

$\begin{cases} 15 = 3 I_2 + I_3 \\ 1 = 3 I_3 - 2 I_2 \end{cases}$

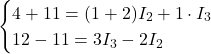
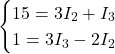
Risoluzione del sistema

Dalla prima equazione:

$I_3 = 15 - 3 I_2$

Sostituendo nella seconda:

$1 = 3(15 - 3 I_2) - 2 I_2 = 45 - 9 I_2 - 2 I_2 = 45 - 11 I_2$

$11 I_2 = 44 \Rightarrow I_2 = \frac{44}{11} = 4\,\text{A}$

Ora calcoliamo:

$I_3 = 15 - 3 \cdot 4 = 3\,\text{A}$

$I_1 = I_2 + I_3 = 4 + 3 = 7\,\text{A}$

Articoli correlati

Esercizo 9: Soluzione

Esercizio 8: Soluzione

Esercizio 7: Soluzione