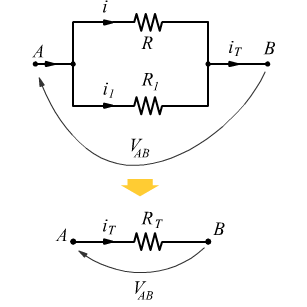
Esercizio risolto: Resistenze in parallelo e corrente totale assorbita
Dati del problema
Nel circuito seguente, la corrente che attraversa la resistenza R è i = 6\,A e va dal morsetto A al morsetto B.
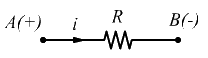
Sono noti i potenziali dei punti A e B:
La corrente totale assorbita dal carico è ![]() .
.
Obiettivo: determinare il valore della resistenza ![]() e il valore di una resistenza
e il valore di una resistenza ![]() , collegata in parallelo a
, collegata in parallelo a ![]() , in modo che la corrente totale sia 10 A.
, in modo che la corrente totale sia 10 A.
Soluzione passo passo
1. Calcolo della resistenza 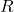
Differenza di potenziale:
![]()
Applicando la legge di Ohm:
![]()
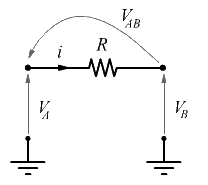
2. Inserimento di una resistenza in parallelo 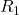
Con la resistenza ![]() in parallelo a
in parallelo a ![]() , la corrente totale è
, la corrente totale è ![]() , e la tensione ai capi resta
, e la tensione ai capi resta ![]() .
.
Resistenza equivalente del circuito:
![]()
3. Calcolo della 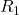
La formula della resistenza equivalente per due resistori in parallelo è:
![]()
Sostituendo i valori:
![]()
Risolvendo l’equazione:
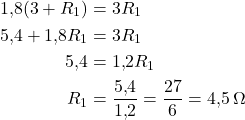
Risultati finali