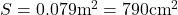Calcolo della capacità e dell’area delle armature di un condensatore piano
Tra le armature di un condensatore piano è applicata una tensione:
![]()
Sapendo che la carica è:
![]()
e che il mezzo interposto è l’aria, calcoliamo:
-
la capacità del condensatore;
-
l’area delle armature sapendo che la distanza tra esse è:
![]()
1. Calcolo della capacità
Dalla formula:
![]()
Quindi:
![]()
2. Permittività dell’aria
Poiché il dielettrico è aria:
![]()
3. Calcolo dell’area delle armature
Dalla formula della capacità di un condensatore piano:
![]()
Sostituendo i valori:
![]()
Convertendo in centimetri quadrati:
![]()
Risultato finale
-
Capacità del condensatore:
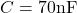
-
Area delle armature: