🔹 Soluzione:
-
Totale delle coppie possibili (con ripetizione):
Ogni dado ha 6 facce: {1, 2, 3, 4, 5, 6}.
Lanciando due dadi, il numero totale di coppie è dato da: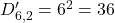
(cioè ogni faccia del primo dado può essere associata a ognuna delle 6 facce del secondo)
-
Coppie con entrambi i numeri dispari:
I numeri dispari tra 1 e 6 sono: {1, 3, 5}, quindi 3 numeri.
Il numero di coppie con solo numeri dispari è: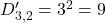
🎲 Tutte le 36 coppie:
![\[ \begin{array}{cccccc} (1,1) & (1,2) & (1,3) & (1,4) & (1,5) & (1,6) \\ (2,1) & (2,2) & (2,3) & (2,4) & (2,5) & (2,6) \\ (3,1) & (3,2) & (3,3) & (3,4) & (3,5) & (3,6) \\ (4,1) & (4,2) & (4,3) & (4,4) & (4,5) & (4,6) \\ (5,1) & (5,2) & (5,3) & (5,4) & (5,5) & (5,6) \\ (6,1) & (6,2) & (6,3) & (6,4) & (6,5) & (6,6) \\ \end{array} \]](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-12054de86a6e91d53ec93e6b8e4c0f1e_l3.png "Rendered by QuickLaTeX.com")
🔸 Coppie con entrambi i numeri dispari:
I numeri dispari sono {1, 3, 5}, quindi:
![\[ \begin{array}{ccc} (1,1) & (1,3) & (1,5) \\ (3,1) & (3,3) & (3,5) \\ (5,1) & (5,3) & (5,5) \\ \end{array} \]](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-48a72be218b4d4acbbbb3fb95d468a49_l3.png "Rendered by QuickLaTeX.com")
Totale: 9 coppie con entrambi i numeri dispari ✅
✅ Risposta finale:
- Totale delle coppie: 36
- Coppie con due numeri dispari: 9