Un esempio introduttivo
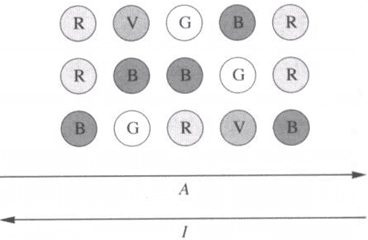
Proviamo a descrivere usando uno schema grafico, il seguente problema. Abbiamo a che fare con tre luci che si accendono con colori ad intermittenza secondo il seguente schema.
All’interno dei cerchi, che descrivono le luci, c’è il simbolo per il relativo colore, R per rosso, B per Blu, V per verde, G per giallo. Ad intervalli di tempo fissati ci si sposta di una posizione nella sequenza, passando, ad esempio, da rosso, rosso, blu della prima terna verticale di luci al verde, blu, giallo della seconda e così via. La sequenza può essere percorsa anche in senso inverso (A per avanti, I per indietro) a seconda del valore di un segnale di controllo esterno. Come nei semafori è possibile interrompere il funzionamento con un segnale esterno, chiamiamolo Stop, facendo diventare «nere» le luci e far riprendere il funzionamento con il segnale Start.Tutto ciò può essere espresso in maniera sintetica nel diagramma di figura.Ognuno dei cerchi nella figura rappresenta uno stato possibile di funzionamento del sistema che vogliamo rappresentare. Al loro interno abbiamo scritto un nome rappresentativo dello stato e i colori delle tre luci che indicano l’uscita del nostro sistema. Al centro è inserito lo stato iniziale del sistema corrispondente alle luci spente. Seguendo la freccia in uscita da esso, segnale di Start, giungiamo in un nuovo stato, lo stato 1 corrispondente alla prima sequenza di luci. Si compie così una transizione di stato in risposta ad un segnale d’ingresso. A seconda poi che in ingresso ci sia A oppure I ci si sposta da stato a stato percorrendo la sequenza luminosa in un verso oppure nell’altro. Nel momento in cui da uno qualsiasi dei vari stati sia sentito in ingresso il segnale Stop si ritorna nello stato spento.
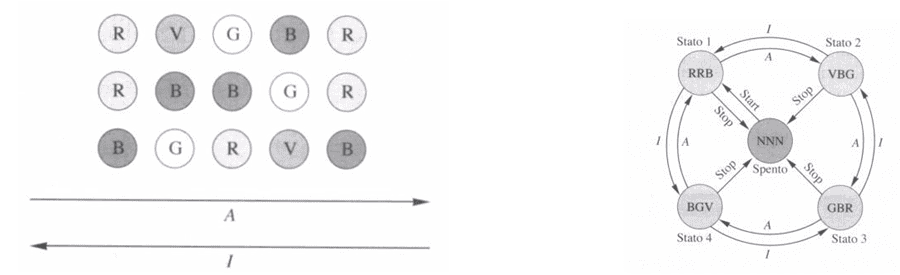
In questo modo abbiamo dato una descrizione tramite un modello formale del funzionamento del nostro sistema. Tale tipo di modello si chiama Automa a Stati Finiti di Moore. Esso è definito rigorosamente da tre insiemi e da due applicazioni tra questi insiemi.
Insieme d’ingresso I: definisce i valori possibili per l’ingresso all’automa.
Insieme di stato S: definisce i possibili stati in cui può trovarsi a funzionare il sistema oggetto di studio.
Insieme d’uscita U: definisce i possibili valori per le uscite.
Transizione di stato: è l’applicazione che dato lo stato in cui si trova il sistema ed i valori degli ingressi determina il prossimo stato del sistema. Sono le frecce presenti nel diagramma.
Transizione d’uscita: è l’applicazione che stabilisce a seconda dello stato in cui si trova il sistema quanto vale l’uscita.
Nell’esempio considerato, quindi, avremo:
I = {Start,Stop,I,A}
U = {R,B,G,V,N}
S = {spento,Stato1,Stato2,Stato3,Stato4}
| Transizione di stato | Valori d’ingresso | ||||
| Start | Stop | A | I | ||
| Stato attuale | Spento | Stato1 | … | … | … |
| Stato1 | … | Spento | Stato2 | Stato4 | |
| Stato2 | … | Spento | Stato3 | Stato1 | |
| Stato3 | … | Spento | Stato4 | Stato2 | |
| Stato4 | … | Spento | Stato5 | Stato3 | |
Mediante la tabella, conoscendo i valori d’ingresso e lo stato attuale, possiamo determinare i valori dello stato futuro. Se, osservando il diagramma, l’automa è attualmente nello stato S2 e gli si fornisce in ingresso il valore A, seguendo la transizione indicata dalla freccia associata ad A, l’automa si sposta nello stato S3. Tale informazione viene riportata nella tabella, così di seguito la si completa. In alcuni casi non è prevista la freccia in uscita dagli stati in corrispondenza di alcuni ingressi e dunque si lascia incompleta la relativa casella. In altri termini la transizione di stato può essere una trasformazione non completamente definita.
| Stato | Uscita luce 1 | Uscita luce 2 | Uscita luce 3 |
| Spento | N | N | N |
| Stato1 | R | R | B |
| Stato2 | V | B | G |
| Stato3 | G | B | R |
| Stato4 | B | G | V |
Vediamo ora la trasformazione d’uscita:
In questa tabella, lo stato in cui si trova il sistema determina il valore delle tre uscite.
L’automa a stati finiti di Moore è dunque uno schema corrispondente al modello astratto di figura.
La freccia che torna indietro rappresenta il fatto che il nuovo stato dipende da quello attuale, il sistema ha memoria del suo passato.
A parità d’ingresso l’uscita può essere diversa come si vede dalle tabelle.

Confronto tra sistemi combinatori e sistemi sequenziali
Vediamo, per fare un confronto tra ciò che è descritto da un automa e ciò che può essere descritto dall’algebra di Boole, di costruire un modello di un semplice sistema descritto in termini di tabelle di verità e di darne una rappresentazione analoga all’ultimo schema visto per gli automi.

La figura rappresenta schematicamente un elemento di un indicatore di numeri: il display a sette segmenti. A seconda di come le varie parti componenti il display siano illuminate o meno riusciamo a rappresentare le varie cifre.
Accendendo i segmenti 2 e 3 visualizziamo un 1, accendendo 1,2,7,5,4 otteniamo il 2, accendendo 1,2,7,3 e 4 otteniamo il 3 e così via per gli altri numeri.
Se rappresentiamo l’acceso–spento con V e F possiamo rappresentare il funzionamento del display con una tabella del tipo:
| Uscite | |||||||
| Ingressi |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | V | V | V | V | V | V | F |
| 1 | F | V | V | F | F | F | F |
| 2 | V | V | F | V | V | F | V |
| 3 | V | V | V | V | F | F | V |
| 4 | F | V | V | F | F | V | V |
| 5 | V | F | V | V | F | V | V |
| 6 | V | F | V | V | V | V | V |
| 7 | V | V | V | F | F | V | F |
| 8 | V | V | V | V | V | V | V |
| 9 | V | V | V | V | F | V | V |
Lo schema completo del circuito per la codificazione dei numeri è il seguente:

Con questa tabella descriviamo il comportamento di un sistema con un ingresso a 10 possibili valori e 7 uscite. Lo schema del sistema potrebbe essere come quello di figura.
A differenza dello schema del controllore di sequenze luminose, non si ha un percorso di ritorno verso l’ingresso.

Ciò significa che in questo caso non si ha memoria del funzionamento precedente, in altri termini la combinazione in ingresso determina univocamente il valore delle uscite. Un sistema di questo tipo, descrivibile in termini di tavole di verità si dice combinatorio. Un sistema viceversa descritto da un automa si dice sequenziale. Infatti è la sequenza dei vari ingressi ricevuti nel passato che ha determinato l’ultimo stato del sistema che determina il valore dell’uscita.
Gli automi di Mealy
Vediamo ora un altro esempio di sistema che ci porterà a definire il concetto di Automa a stati finiti di Mealy.
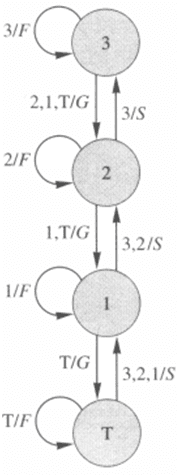
Con il diagramma di figura schematizziamo il funzionamento di un ascensore.

I quattro stati T,1,2,3 rappresentano i possibili piani a cui l’ascensore può trovarsi. Le frecce, come nel caso di automa di Moore, rappresentano transizioni tra stati. Al loro fianco compaiono non solo i valori degli ingressi possibili 1,2,3,T ma anche il valore dell’uscita del sistema, in questo caso l’informazione per il motore che pilota l’ascensore di spingere in alto S, tirare in basso G o stare fermo F. Se si segue lo schema si comprenderà la logica dell’automa. Supponiamo di essere al secondo piano. Se arriva il segnale 3 ci si sposta al terzo piano dando al motore il comando per salire, se qualcuno preme il tasto 2 si resta fermi dicendo al motore di stare fermo, se viene premuto uno dei due tasti 1,T ci si sposta in basso fino a raggiungere il piano desiderato dicendo al motore di calare in basso. A differenza del caso di Moore non è lo stato a determinare il valore dell’uscita, ma è la transizione a determinarla.
Essendo la transizione definita dalla coppia stato di partenza/ingresso, anche l’uscita dipende da questa coppia di valori.
I: Insieme degli ingressi
S: Insieme degli stati
U: Insieme delle uscite
Transizione di stato: un’applicazione che fa corrispondere alla coppia stato attuale – ingresso lo stato futuro.
Transizione d’uscita: un’applicazione che fa corrispondere alla coppia stato attuale – ingresso l’uscita.
Lo schema generale dell’automa potrebbe essere il seguente:
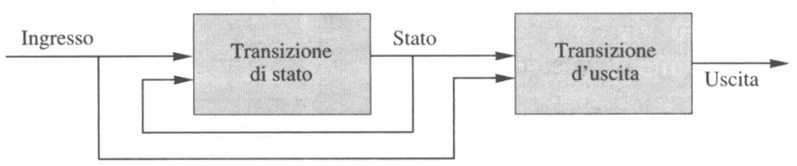
Vediamo nel nostro caso cosa succede:
I = {1,2,3,T}
S = {1,2,3,T}
U ={S,G,F}
Transizione di stato e transizione d’uscita sono definite da un’unica tabella:
| Ingressi | ||||
| Stato_attuale | 1 | 2 | 3 | T |
| 1 | 1/F | 2/S | 2/S | T/G |
| 2 | 1/G | 2/F | 3/S | 1/G |
| 3 | 2/G | 2/G | 3/F | 2/G |
| T | 1/S | 1/S | 1/S | T/F |
Valutazione della capacità di applicazione e approfondimento
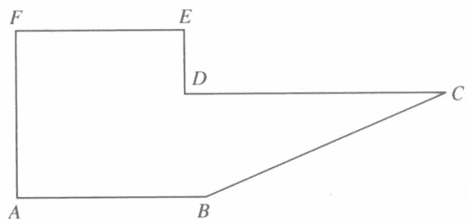
Si vuole descrivere il funzionamento di un dispositivo automatico in grado di pilotare il movimento di un attrezzo lungo il percorso indicato nel disegno. Il movimento in un piano è controllabile tramite due motori: uno destinato a generare il movimento lungo l’asse X, l’altro lungo l’asse Y. Ad esempio, se l’attrezzo è posizionato in A per poterlo spostare in B si deve ordinare al motore dell’asse delle X di generare uno spostamento a destra, mentre al motore delle Y si ordinerà di non generare movimento. Poi per passare in C bisognerà ordinare un movimento a destra ed uno in alto. Così è possibile pensare di controllare il moto tra i vari vertici. Si supponga inoltre che sia necessario dover indicare il verso di percorrenza con un segnale in ingresso corrispondente ai sensi antiorario (A per avanti) ed orario (I per indietro). Si vuole anche far in modo che ci si possa fermare nei vari vertici, dunque un terzo possibile valore dell’ingresso sarà F per fermo. Si individui un automa di Mealy in grado di gestire la situazione
rappresentandolo sia sotto forma di tabella sia sotto forma di diagramma.
Si prenda di nuovo in considerazione il semaforo. Si vogliono aggiungere ad esso ulteriori funzionalità. Innanzi tutto, oltre che a potersi spegnere, deve anche potersi bloccare su una determinata combinazione di luci. Dopo aver eseguito questa modifica, si faccia in modo che sia possibile selezionare l’intensità luminosa della luce emessa dai tre fari tra due livelli: luce forte e luce debole. Si dia una soluzione sia in termini di diagramma sia in termini di tabella.
{/gspeech}
ESERCIZI
- Si fornisca la definizione di automa a stati finiti di Moore.
- Si fornisca la definizione di automa a stati finiti di Mealy.
- Si illustri chiaramente la differenza tra un sistema sequenziale ed un automa.
- Si descriva l’automa ascensore in termini di diagramma e di tabella.
- L’automa per l’ascensore:
q è un automa di Moore.
q è un sistema combinatorio.
q è un sistema senza memoria.
q è un sistema sequenziale.
