Azioni meccaniche tra campi magnetici e correnti

Azioni meccaniche tra campi magnetici e correnti

{gspeech style=2}

Sappiamo che esiste un legame fra correnti elettriche e campi magnetici, nel senso che ogni corrente produce attorno a sé un campo magnetico e quindi esistono tra loro forze attrattive o repulsive.

Più precisamente, una corrente in presenza di un campo magnetico dà luogo a forze meccaniche, che sono il principio di funzionamento dei motori.

Per vedere la natura di queste forze, immaginiamo di porre un conduttore percorso da corrente all’interno di un campo magnetico generato da un magnete permanente.

In Figura 1 sono messi in evidenza separatamente dapprima i campi magnetici singoli (del magnete e della corrente) e poi il campo magnetico risultante. In quest’ultimo le linee di campo del magnete e del conduttore, quando sono dirette in senso contrario, tendono ad annullarsi o ad indebolirsi (a sinistra del conduttore).

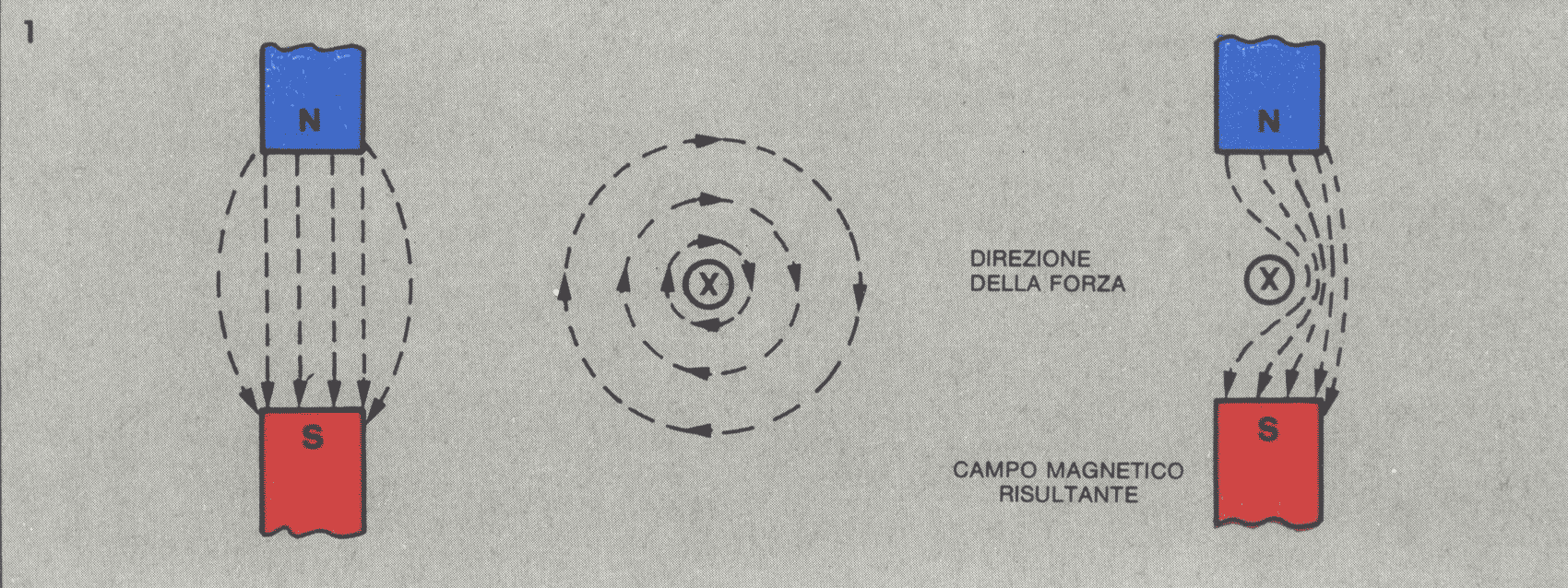
A destra, invece, le linee dei due campi sono dirette nello stesso senso e quindi il campo totale è rinforzato.

Poiché, il flusso ha tendenza ad essere uniforme nello spazio, il conduttore è sollecitato a spostarsi nella direzione dove si ha minor flusso: ha quindi origine una forza meccanica detta forza elettromagnetica, che spinge il conduttore a spostarsi.

Per determinare la direzione in cui agisce la forza, possiamo utilizzare, la regola della mano sinistra o di Fleming: disponendo tre dita della mano sinistra ad angolo retto tra loro, l’indice nel senso del campo ed il medio nel senso della corrente, il pollice dà il verso della forza, cioè del movimento.

L’intensità di questa forza F è proporzionale all’induzione B del campo magnetico (supposto costante in tutto lo spazio dove si muove il conduttore), all’intensità I della corrente e alla lunghezza l della parte di conduttore immersa dentro il campo. Pertanto, l’espressione della forza sarà:

F = B · l · I

dove F si misura in Newton (N), B in Weber per metro quadrato (Wb/m²), l in metri (m) ed I in ampere (A).

Sostituiamo adesso il conduttore immerso nel campo magnetico con una spira percorsa da corrente; ciò equivale ad avere due conduttori paralleli percorsi da correnti uguali e di senso contrario. Per la regola della mano sinistra essi saranno ovviamente portati a muoversi in direzioni opposte con forze di spostamento contemporanee e della stessa intensità. Se la spira è imperniata su un asse girevole, è quindi sollecitata a ruotare, Figura 2.

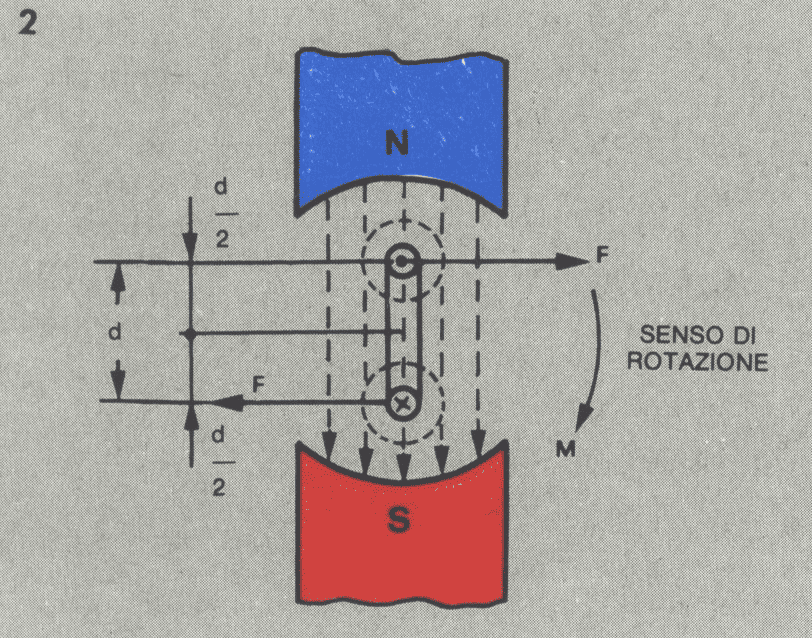
Per definire più esattamente l’azione in questo caso, occorre introdurre una nuova grandezza che chiamiamo coppia di rotazione che meccanicamente dà un movimento. Se F è la forza su un lato della spira immerso nel campo magnetico e è la distanza del punto di applicazione della forza dal punto in cui è imperniata la spira, si ha per questo lato un momento di rotazione pari a .

La coppia di rotazione, che mette insieme il contribuito dei due momenti, secondo la Figura 2, ha lo stesso senso di rotazione, e sarà data da:

Poiché, poi, F = B · l · I si ha pure:

M = B · l · I ·d

misurata in newton per metro (N × m).

Il valore del momento non è costante, ma varia in dipendenza della posizione assunta dalla spira nel campo magnetico: ha valore massimo quando la spira è parallela alle linee di flusso, mentre diventa nullo quando essa, ruotando, è perpendicolare alle linee del campo.

Tutte le altre posizioni avranno valori intermedi.

In generale, allora, il valore del momento dipende, oltre che dalle condizioni poste alla partenza, dall’angolo formato dalla spira con le linee di flusso. Nella posizione iniziale con angolo pari a zero e con momento massimo, il flusso che attraversa la spira è nullo, mentre è massimo quando la spira è perpendicolare al campo.

Possiamo allora dire che una spira entro un campo magnetico e percorsa da corrente, tende a ruotare per disporsi in modo da essere attraversata dal massimo flusso.

Da quello che abbiamo visto, si può concludere dicendo che la forza o il momento nascono quando c’è la presenza di un flusso magnetico e una corrente interagenti fra loro.

Poiché il flusso magnetico può essere prodotto, come sappiamo, non solo da magneti permanenti, ma anche da conduttori percorsi da corrente, si avranno delle forze meccaniche anche fra questi ultimi. In questo caso diciamo che le forze sono originate da fenomeni elettrodinamici fra conduttori.

La natura delle forze può essere verificata con un ragionamento simile a quello visto per i fenomeni elettromagnetici.

La Figura 3 rappresenta un campo risultante formato da due conduttori paralleli e percorsi da correnti.

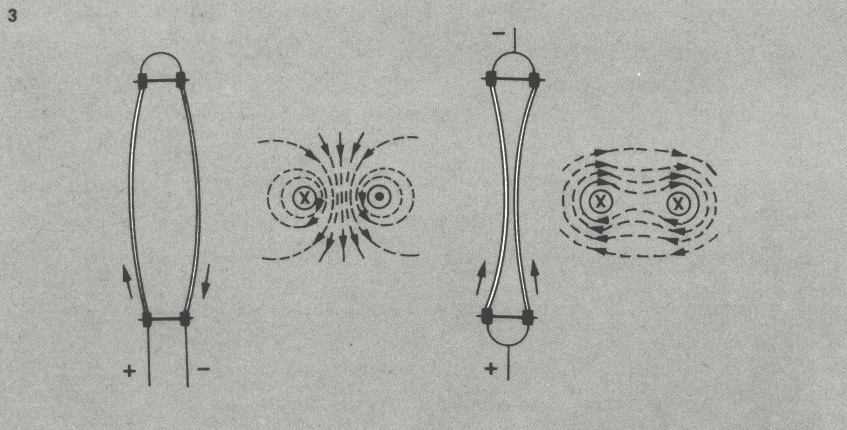
Con direzione di corrente una opposta dall’altra, si forma fra i due conduttori un campo rinforzato a causa delle linee interne che hanno uguale direzione, mentre all’esterno un viene indebolito.

Quindi, i due conduttori cercano di distanziarsi (Figura 3 a).

Se le direzioni delle correnti sono uguali (Figura 3 b) avviene tutto il contrario: le linee di forza fra i conduttori hanno senso inverso e indeboliscono il campo, mentre all’esterno hanno direzione uguale e lo rinforzano.

I conduttori quindi tendono ad avvicinarsi.

In definitiva abbiamo constatato che: fra due conduttori si genera una forza attrattiva se le correnti sono equiverse e repulsiva se hanno invece sensi contrari.

Possiamo anche dire che i due conduttori tendono a disporsi in modo che risulti massimo il flusso totale concatenato con i due circuiti.

Anche in questo caso il verso della forza si può trovare applicando la regola della mano sinistra. La sua intensità è data dalla formula:

dove rappresenta la permeabilità magnetica del mezzo (di solito aria), entro il quale si svolge il campo, I è la lunghezza utile dei conduttori, cioè il tratto di essi che rimane reciprocamente influenzato, d la loro distanza ed I₁, e I₂ le loro correnti.

Un caso particolare interessante si ha se le due correnti sono uguali. Si ha in tal caso:

ovvero la forza è proporzionale al quadrato della corrente I che percorre i due conduttori: è questo il caso di due spire contigue di un solenoide o di un avvolgimento con spire sovrapposte.

Questa relazione ci dice pure che, mentre per piccole correnti la forza è di entità trascurabile, nel caso di corto circuiti, cioè in situazioni in cui la corrente può raggiungere valori di decine di volte la corrente nominale, la forza assume valori considerevoli; situazione che, per l’appunto, va prevista in fase di costruzione, per esempio, di avvolgimenti di macchine.

Si ovvia all’inconveniente predisponendo robusti ancoraggi agli avvolgimenti.

Quando i conduttori non sono paralleli, le forze sono ancora attrattive per correnti equiverse e repulsive per correnti di sensi opposti: i conduttori, essendo incrociati, tenderanno a ruotare disponendosi paralleli fra loro se si attirano, e ad angolo retto se si respingono, facendo perno sul punto di incrocio. In questo caso si origina una coppia che provoca la rotazione che, come la forza del caso precedente, è ancora proporzionale al prodotto delle due correnti.

Riportiamo un esempio di applicazione dell’espressione della forza elettromagnetica:

Un conduttore rettilineo lungo 20 cm, percorso da una corrente di 8 A, è immerso in un campo magnetico uniforme avente una induzione di 1,2 Wb/m².

Calcolare la forza esercitata sul conduttore.

Si sa che la formula risolutiva è:

F = B·l·I

In cui l è espressa in metri. Si ha allora:

F = 1,2·20·10^-2·8 = 1,92 N

La direzione di questa forza, come è noto, si ricava applicando la regola della mano sinistra.

{/gspeech}