Blog di Megistone

Megistone - Per non perdere l'orientamento

02-Il condensatore

IL CONDENSATORE

Consideriamo un campo elettrico uniforme agente sugli atomi di un isolante. L’effetto che si può osservare è il seguente: il nucleo positivo sarà attratto verso la parte negativa del campo, mentre gli elettroni tenderanno verso quella positiva.

 

 

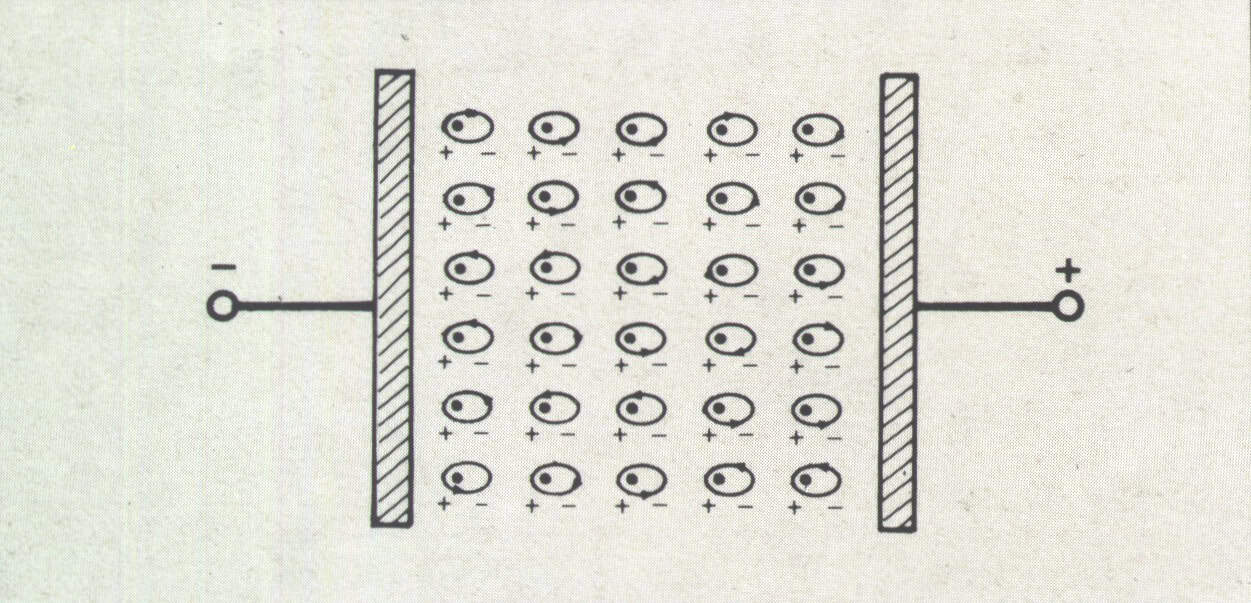
Ogni atomo, pertanto, si presenterà come un piccolissimo corpo che ha da una parte un eccesso di carica positiva e dall’altra un eccesso di carica negativa. Tutto il dielettrico quindi risulterà in uno stato di tensione elettrica chiamata polarizzazione dielettrica.

In altre parole, possiamo dire che, sotto l’effetto di una forza elettrica, l’induzione conseguente polarizza il dielettrico.

Il coefficiente di proporzionalità tra induzione e forza elettrica è chiamato costante dielettrica e caratterizza la natura del dielettrico. Più esattamente definiamo questa come l’attitudine di un corpo isolante a immagazzinare cariche elettriche.

La costante dielettrica viene simbolicamente rappresentata con la lettera greca ε (epsilon) ed è misurata in:

 

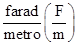
Per il vuoto e praticamente anche per l’aria, il suo valore è:

 

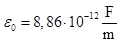
Per gli altri isolanti, solidi o liquidi, si preferisce utilizzare, anziché il valore assoluto ε, troppo complicato, il valore relativo εr, detto costante dielettrica relativa.

 

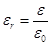
Nella Tabella vengono riportate le costanti dielettriche relative, di alcuni materiali isolanti.

 

Costanti dielettriche relative

Materiale

 εr

Materiale

 εr
Ambra 3 Legno paraffinato 5
Bachelite 6 Mica chiara 6
Carta impregnata per cavi 3 Micanite 5
Carta manila 2 Olio da trasformatori 2,5
Carta paraffinata 4 Presspan 4,5
Celluloide 3 Paraffina 2
Ebanite 3 Porcellana 5
Fibra rossa 2 Tela sterlingata 4,5
Gomma vulcanizzata 3 Vetro in lastra 6

Il campo elettrico considerato finora, si ottiene in pratica fra due lamine metalliche, dette armature, separate tra loro da un isolante solido, liquido o gassoso. Un sistema del genere è in grado di immagazzinare energia elettrostatica, quando viene alimentato da una tensione continua, e prende il nome di condensatore, rappresentato simbolicamente con due tratti di linea paralleli.

 

 

Si definisce capacità di un condensatore, e si indica con C, il rapporto tra la carica elettrica Q sulle armature e la tensione V applicata:

 

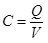
Questo parametro esprime attitudine di un condensatore ad accumulare cariche elettriche e quindi energia nel dielettrico. La sua unità di misura è il farad (simbolo F): un condensatore ha la capacità di 1 farad quando, applicando la tensione di 1 V alle sue armature, esse assumono la carica di 1 coulomb.

In pratica un simile condensatore è irrealizzabile. Si tratta infatti di un valore molto elevato, per cui di solito vengono usati i suoi sottomultipli: microfarad, nanofarad e picofarad.

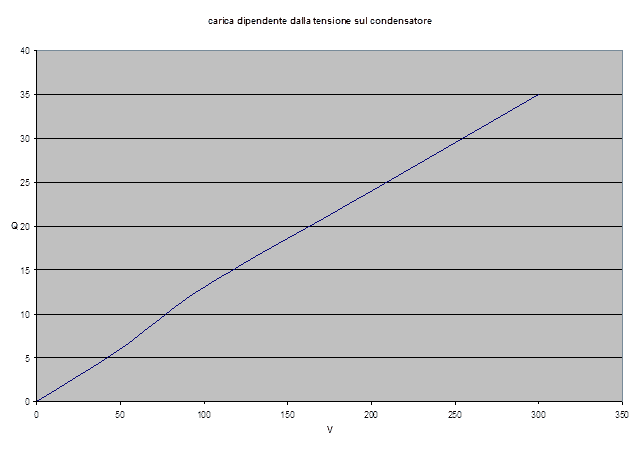
Tale legge induce ad una riflessione: quanto maggiore è la capacità, tanto maggiore è la quantità di carica accumulate. Carica e capacità sono quindi proporzionali.

Q ~ C

o

Q = C·V

 

Finora non si è mai esaminato che tipo di rapporto ci sia tra struttura del condensatore e la sua capacità. Lo facciamo ora.

Il condensatore è fondamentalmente formato da due piastre conduttrici che si trovano a una data distanza. Le superfici delle piastre e la loro distanza vengono perciò ad esercitare un’influenza sulla capacità.

La dipendenza della capacità dalla superficie può essere spiegata attraverso alcune riflessioni.

Se si aumenta la superficie del condensatore c’è più spazio a disposizione per le cariche. La capacità è quindi proporzionale alla superficie:

 

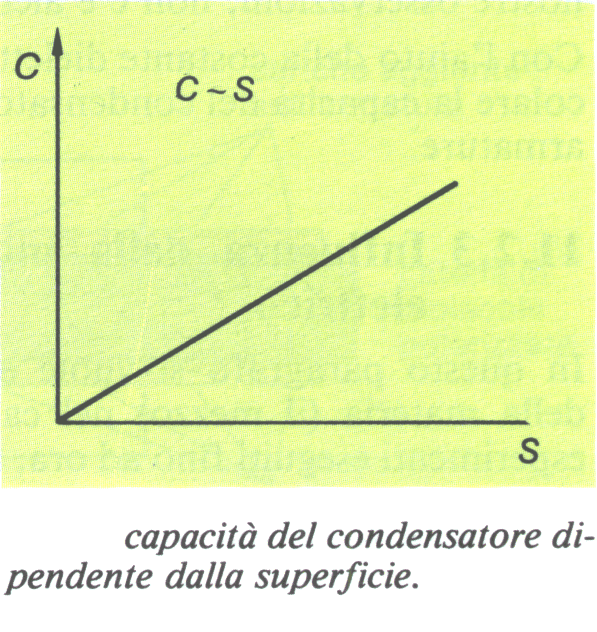
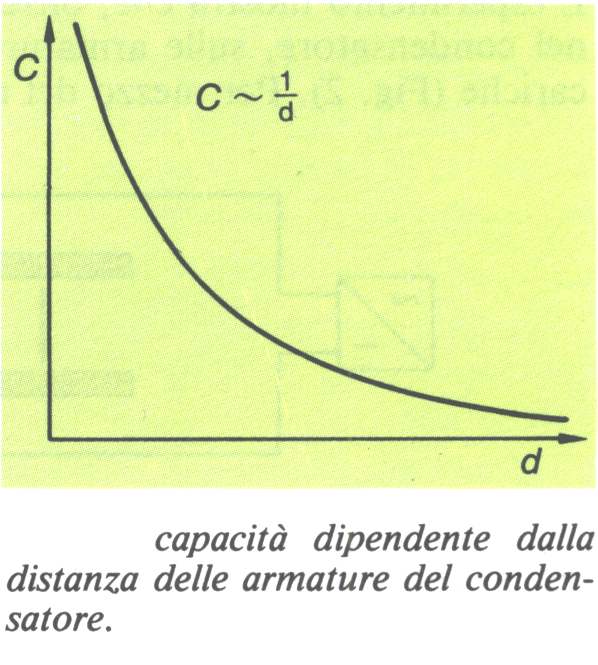
Inoltre si dimostra che la capacità aumenta con la diminuzione della distanza, perché sulle armature si accumulano più cariche. Un aumento della distanza comporta una diminuzione della capacità.
Ricerche più precise portano alla proporzione:

 

 

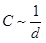
Se si riuniscono le due proporzioni, si ottiene:

 

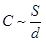
Questa relazione non può ancora essere scritta sotto forma di equazione, perché valore numerico e unità di misura non concordano ancora.

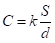
Con k pari alla costante dielettrica assoluta.

Riassumendo, la capacità di un condensatore ad armature piane è:

  • direttamente proporzionale alla superficie affacciata della armature (S);
  • inversamente proporzionale alla distanza (d) tra le armature;
  • dipendente dalla natura del dielettrico interposto fra le armature (costante dielettrica ε).

Si può quindi scrivere:

 

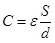
Agendo sui parametri detti si possono ottenere, perciò, condensatori di capacità diverse e si può altresì comprendere il criterio che ha guidato nella realizzazione dei vari tipi: normalmente si cerca di ottenere i massimi valori di capacità con il minimo volume.

Riportiamo ora un semplice esempio di calcolo che mette in evidenza e chiarisce ulteriormente quanto appena detto.

Esercizio: Condensatore a lastre piane e variazione della distanza
Un condensatore a lastre piane parallele, tra loro distanti 5 mm e con superficie di 400 cm² per armatura, è collegato ad una tensione di 500 V.

1. Calcolo della capacità
Utilizziamo la formula della capacità di un condensatore piano:

C = \varepsilon_0 \cdot \frac{A}{d}

Dove:

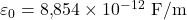  • \varepsilon_0 = 8{,}854 \times 10^{-12} \ \text{F/m} (costante dielettrica del vuoto)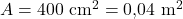
  • A = 400 \ \text{cm}^2 = 0{,}04 \ \text{m}^2
  • d = 5 \ \text{mm} = 5 \times 10^{-3} \ \text{m}

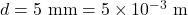
Calcoliamo:

C = 8{,}854 \times 10^{-12} \cdot \frac{0{,}04}{5 \times 10^{-3}} = 7{,}0832 \times 10^{-11} \ \text{F} = \boxed{70{,}8 \ \text{pF}}

2. Calcolo della carica elettrica assorbita
Utilizziamo la formula:

Q = C \cdot V

Con V = 500 \ \text{V} , otteniamo:

Q = 7{,}0832 \times 10^{-11} \cdot 500 = 3{,}5416 \times 10^{-8} \ \text{C} = \boxed{35{,}4 \ \text{nC}}

3. Le piastre vengono allontanate a 2 cm
Dopo aver scollegato il condensatore dalla linea di tensione, le due armature vengono portate ad una distanza di 2 cm:

d_2 = 2 \ \text{cm} = 2 \times 10^{-2} \ \text{m}

Poiché il condensatore è isolato, la carica resta costante, ma la capacità cambia:

C_2 = \varepsilon_0 \cdot \frac{A}{d_2} = 8{,}854 \times 10^{-12} \cdot \frac{0{,}04}{2 \times 10^{-2}} = 1{,}7708 \times 10^{-11} \ \text{F} = \boxed{17{,}71 \ \text{pF}}

4. Nuova d.d.p. tra le armature
Con Q costante:

V_2 = \frac{Q}{C_2} = \frac{3{,}5416 \times 10^{-8}}{1{,}7708 \times 10^{-11}} = \boxed{2000 \ \text{V}}

5. Inserimento di una lastra di vetro tra le piastre
Si interpone ora tra le due piastre una lastra di vetro di spessore 20 mm, con costante dielettrica relativa:

\varepsilon_r = 6

Nuova capacità con dielettrico:

C' = \varepsilon_0 \varepsilon_r \cdot \frac{A}{d} = 8{,}854 \times 10^{-12} \cdot 6 \cdot \frac{0{,}04}{0{,}02} = 1{,}06248 \times 10^{-10} \ \text{F} = \boxed{106{,}25 \ \text{pF}}

La carica rimane invariata:

Q = 3{,}5416 \times 10^{-8} \ \text{C}

Nuova differenza di potenziale:

V' = \frac{Q}{C'} = \frac{3{,}5416 \times 10^{-8}}{1{,}06248 \times 10^{-10}} = \boxed{333{,}3 \ \text{V}}

Conclusione finale

  • Capacità iniziale: 70{,}8 \ \text{pF}
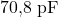
  • Capacità dopo allontanamento: 17{,}71 \ \text{pF}
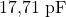
  • Capacità con dielettrico: 106{,}25 \ \text{pF}
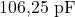
  • D.d.p. iniziale: 500 \ \text{V}
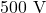
  • D.d.p. dopo allontanamento: 2000 \ \text{V}
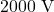
  • D.d.p. con dielettrico inserito: 333{,}3 \ \text{V}

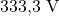
Il dielettrico aumenta la capacità e riduce la tensione, mantenendo costante la carica. Tipico caso di trasformazione a carica costante.

Grandezze caratteristiche dei condensatori
Le caratteristiche dei condensatori sono indicate da grandezze specifiche. Importanti sono la capacità nominale, la tolleranza, la tensione nominale e la resistenza d’isolamento.

Capacità nominale e tolleranza
Con il termine capacità nominale si definisce la capacità assunta dal condensatore a 20°. La gradazione delle capacità nominali avviene secondo la serie IEC (International Electrotechical Commission).

La capacità nominale può essere indicata in modo diverso:

  • valore numerico con unità di misura completa;
  • valore numerico con unità di misura abbreviata;

esempi: 6n8 significa 6,8 nF; 39μ significa 39 μF;

  • valori numerici senza unità di misura;
  • al valore numerico indicato appartiene l’unità di misura pF o μ
  • contrassegno colorato.

Il valore reale della capacità può allontanarsi dal valore nominale per la tolleranza abituale.

Esempio: capacità nominale 22 nF, tolleranza ± 10%.

Da ciò si ottiene un campo di capacità di 22 nF ± 2,2 nF, cioè da 19,8 nF a 24,2 nF.

Tensione nominale
La tensione nominale dei condensatori non può essere superata in nessun caso, perché sussiste il rischio di perforazione del condensatore. La tensione nominale è la tensione continua più alta o il valore massimo di una tensione alternata, che può essere applicata costantemente al condensatore a 40°C di temperatura ambiente.
Anche questo valore viene indicato o direttamente come valore numerico o indirettamente per mezzo di lettere alfabetiche minuscole, oppure per mezzo di un contrassegno colorato.

Tabella:contrassegno con lettere minuscole della tensione nominale dei condensatori

 

 

lettere
minuscole

V

in V
a 50 –
b 125 –
c 160 –
d 250 –
e 350 –
f 500 –
g 700 –
h 1000 –
u 250 ~
v 350 ~
w 500 ~

Le tolleranze dei condensatori sono indicate come segue:

  • impresse direttamente,
  • contrassegnate con colori,
  • contrassegnate con lettere alfabetiche maiuscole.

Esempi di contrassegni di condensatori:

0,47 M 250

0,47 = capacità nominale 0,47 μF

M = tolleranza 20%

250 = tensione nominale 250 V

22 n K d

22 n =capacità nominale 22 nF

K = tolleranza ± 10%

d = tensione nominale 250 V

Tabella: contrassegno con lettere maiuscole delle tolleranze dei condensatori

lettera

maiuscola

tolleranza

C> 10 pF in %
D ± 5
F ± 1
G ± 2
H ± 2,5
J ± 5
K ± 10
M ± 20
N ± 30
P + 100– 0
Q + 30– 10
R + 30– 20
S + 50– 20
T + 50– 10
Z + 100– 20

Resistenza d’isolamento
I condensatori sono accumulatori di cariche. Essi non trattengono però a lungo le loro cariche perché il dielettrico non è un isolante ideale.
Il dielettrico agisce quindi come una resistenza inserita in parallelo.
Dai costruttori non viene indicata la resistenza d’isolamento ma il prodotto di Ris e C. La grandezza è la costante di tempo τ. Essa ci informa su come avviene l’autocaricamento del condensatore.

 

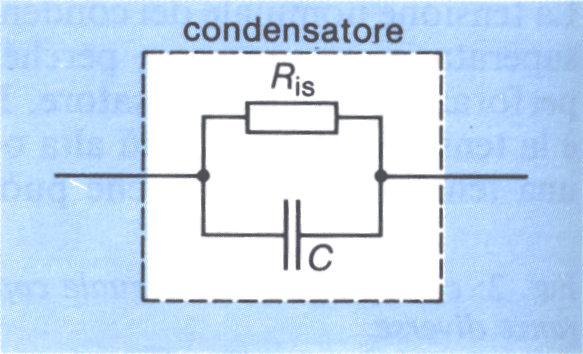
Strutture dei condensatori
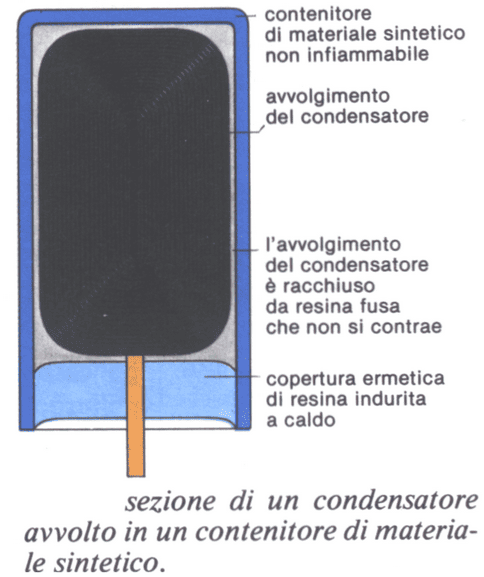
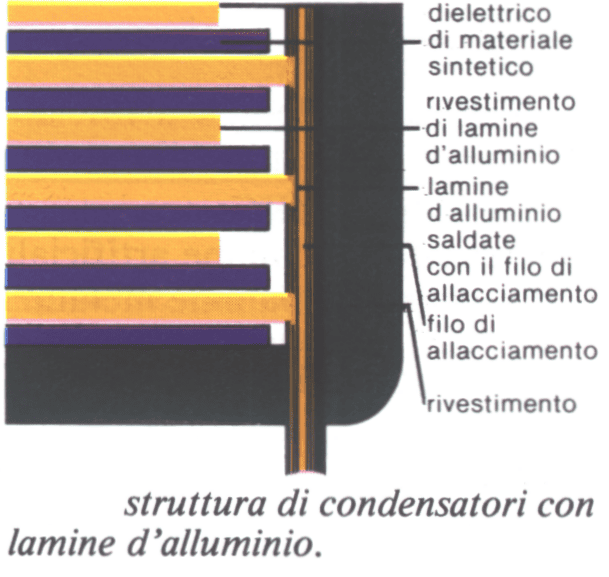
La struttura base dei condensatori viene spiegata mediante schemi. Per aumentare la capacità spesso vengono prodotte armature sotto forma di lamine di metallo (fogli di alluminio). Avvolte,con i corrispondenti materiali di isolamento, si inseriscono poi in scatole di forma quadrata o cilindrica.
In tal modo si ha una superficie utile molto maggiore, e di conseguenza una capacità molto più grande, che in un condensatore piano. Nell’avvolgimento, poi, le armature agiscono elettricamente da entrambe le facce, quindi la superficie utile e la capacità vengono raddoppiate.

 

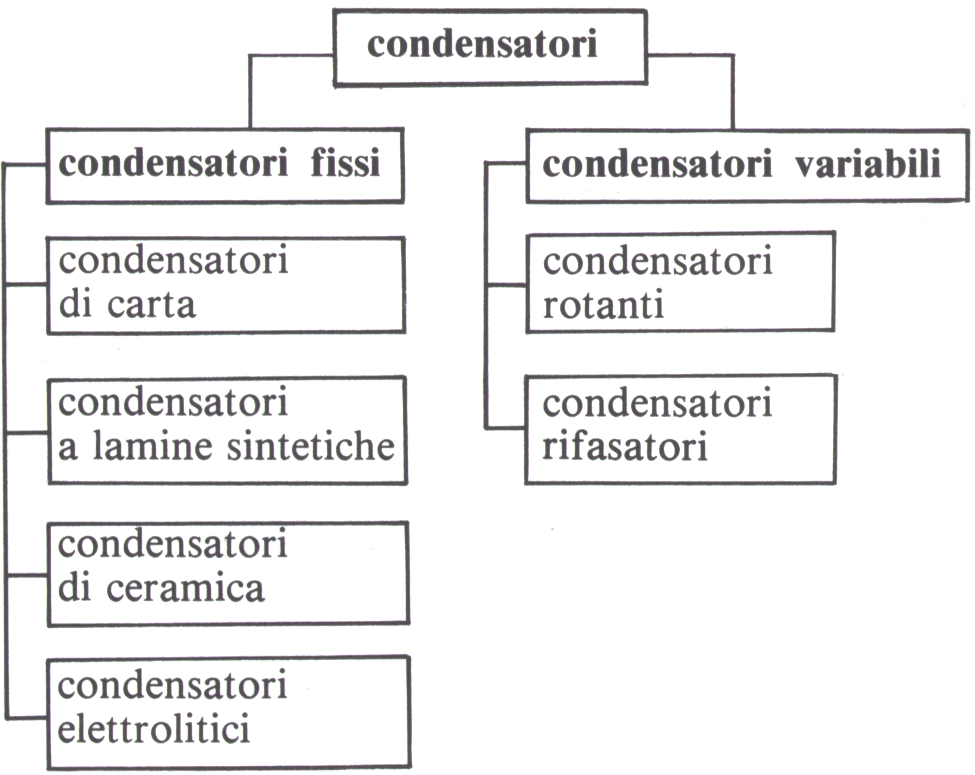
I condensatori, a secondo della loro struttura, si distinguono in condensatori fissi (condensatori con capacità nominale fissa) e in condensatori variabili (con capacità nominale variabile).

I condensatori fissi vengono ulteriormente distinti a seconda del tipo di dielettrico.

 

Condensatori di carta

elettrodi

dielettrico
lamine d’alluminio con spessore da 6 a 7µm carta impregnata (ad esempio, naftalina o paraffina come sostanza impregnante)
oppure
alluminio spruzzato con spessore da 0,02 a 0,05 µm

Una forma particolare di condensatore di carta è il condensatore MP (condensatore di carta metallizzata). Sul dielettrico (carta) è spruzzato uno strato di metallo straordinariamente sottile.
Se nel condensatore MP si verifica una scarica, a causa di un arco voltaico lo strato metallico del dielettrico brucia più rapidamente. Viene così isolata la parte difettosa. Si «autocicatrizza» da solo.
Il tempo di «autocicatrizzazione» è inferiore ai 10 μs.
Vengono usati come condensatori di accoppiamento di potenza di livellamento, per avviamento ed azionamento di motori.

 

Condensatori a lamine sintetiche

Le materie sintetiche si possono lavorare in lamine più sottili della carta. I condensatori a lamine sintetiche sono perciò più piccoli di quelli di carta.

 

elettrodi

dielettrico
lamine d’alluminio lettera di riconoscimento K materie sintetiche lettere di riconoscimento
oppure  
alluminio spruzzato, lettera di riconoscimento MK policarbonato C
polipropilene P
polistirolo S
politereftalico T
acetato di cellulosa U

Esempi:

Contrassegno KS:

condensatore a lamine artificiali con dielettrico di polistirolo e con lamine di metallo come elettrodi.

Contrassegno MKC:

condensatore a lamine artificiali con un dielettrico di policarbonato e lamine metallizzate come elettrodi.

Condensatori di ceramica

elettrodi

 dielettrico

strato metallico, lamine metalliche

masse di ceramica

(ceramica ad ossido)

· condensatori NDK (condensatori con bassa costante dielettrica relativa εr: da 13 a 470),

· condensatori HDK (condensatori con alta costante dielettrica relativa εr: da 470 a 50 000)

Questi condensatori ad alta costante dielettrica relativa possono essere costruiti in dimensioni molto ridotte. Secondo la forma esistono condensatori a disco, tubolari, a sfera e verticali. Vengono prevalentemente usati in radiotecnica ed in elettronica specialmente dove si dispone di pochissimo spazio.

 

Condensatori elettrolitici d’alluminio

Questi condensatori si differenziano completamente da quelli descritti fino ad ora.

 

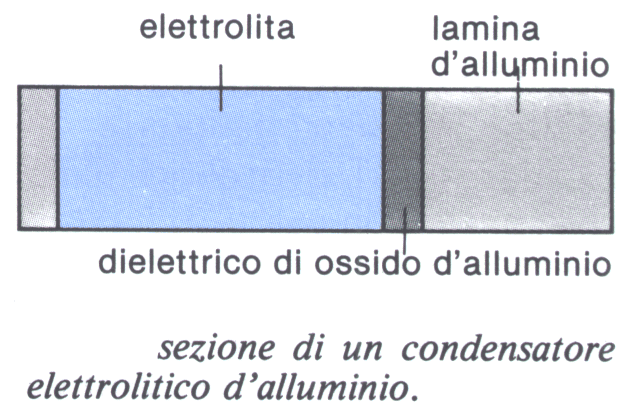
Un elettrodo è d’alluminio, mentre l’altro è costituito da un elettrolita, con contatto verso l’esterno mediante un collegamento metallico (lamina d’alluminio).

Nella costruzione viene inserito tra gli elettrodi uno strato di ossido. Esso è molto sottile (circa 1,2 nm per volt) e si forma solo quando il polo positivo del generatore di tensione si trova nell’elettrodo.

 

Se nell’uso viene effettuata una polarizzazione sbagliata lo strato viene lentamente distrutto.

Nell’allacciamento di un condensatore elettrolitico si deve fare attenzione alla polarità.

elettrodo 1

(anodo)

dielettrico

elettrodo 2

(catodo)
lamined’alluminio

come polo

positivo

 ossidod’alluminio

(ossidazione

anodica),

prodotto elet-

troliticamente

 liquidoelettrolitico

(carta impregnata)

come

polo negativo

In ogni condensatore elettrolitico scorre in pratica una corrente limitata. Questa corrente è necessaria per conservare lo strato d’ossido del dielettrico (corrente residua).

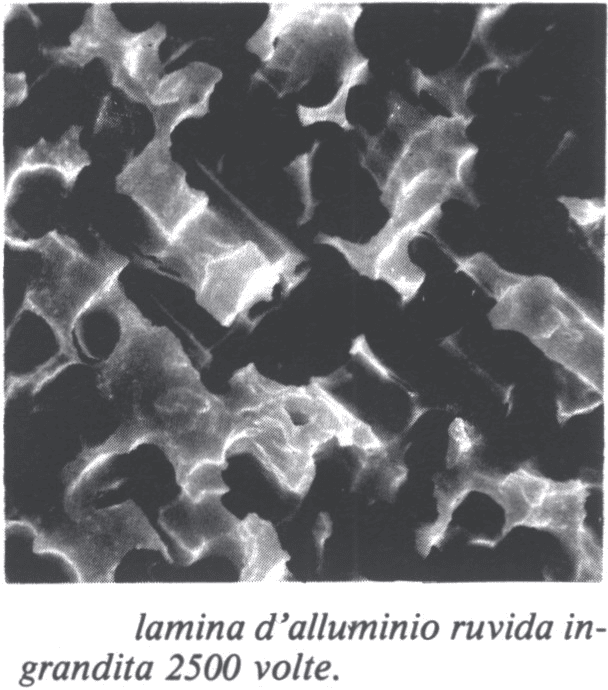
La capacità dipende oltre che dalla distanza dagli elettrodi, anche dall’estensione della superficie.

Per questo motivo spesso nei condensatori elettrolitici le superfici vengono rese più ruvide. Esse diventano così più estese.

Si possono avere condensatori polarizzati e non polarizzati a seconda se il catodo (–) è costituito da un foglio di alluminio non chimicamente ossidato oppure è preparato chimicamente come l’anodo (+). Il tipo polarizzato può essere usato solo per tensioni continue, mentre quello non polarizzato necessita di un volume doppio di uno avente le stesse prestazioni, ma polarizzato. I condensatori elettrolitici vengono usati per livellare le correnti pulsanti continue, per accoppiamento in col­legamenti con transistori, per avviamento di motori.

Condensatori elettrolitici tantalici

I condensatori elettrolitici tantalici sono condensatori elettrolitici i cui anodi sono di tantalio.

 

I condensatori tantalici sono molto piccoli e hanno caratteristiche migliori rispetto a quelli elettrolitici d’alluminio. Il motivo è da ricercarsi nelle ottime qualità dello strato d’ossido.

elettrodo 1

(anodo)

dielettrico

elettrodo 2

(catodo)

· materiale sinterizzato di polvere tantalica

oppure

· lamina tantalica come polo positivo

 strato di ossido tantalico (ossidazione anodica), prodotto elettrochimicamente ossido metallico fisso e semiconduttore(ad esempio, ossido

di manganese) oppure elettrolita liquido (acido) come polo negativo

Vantaggi nei confronti del condensatore elettrolitico d’alluminio:

  • strati d’ossido sottili da 4 nm a 500 nm,
  • costante dielettrica più alta εr ~ 30,
  • se si rende più ruvida la superficie, la capacità viene aumentata di circa 40 volte,
  • corrente residua limitata.

I condensatori elettrolitici tantalici sono contrassegnati anche con colori. L’indicazione della capacità è in μF.

Condensatori variabili

Questi condensatori hanno spesso aria come dielettrico.

 

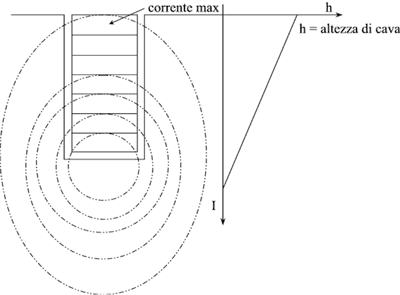
Un tale condensatore si trova, ad esempio, negli apparecchi radio. Il condensatore rotante serve in essi per una precisa individuazione delle stazioni da ricevere. Un gruppo di piastre mobili d’alluminio (rotore) viene inserito nel pacchetto di piastre fisse (statore). I condensatori rotanti vengono inseriti nei circuiti con capacità variabile da 15 pF fino a 550 pF.

 

Accanto ai condensatori rotanti ci sono altre strutture. La figura seguente mostra alcuni tipi di condensatori rifasatori.

 

Piastre mobili vengono inserite o estratte. La capacità perciò varia.

Andamento della corrente e della tensione nel condensatore

Poiché un condensatore ha capacità di immagazzinare energia, può essere utilizzato in pratica come sorgente di energia per un certo periodo di tempo, dopodiché dovrà nuovamente essere ricaricato. Si hanno quindi due fasi, una di carica e una di scarica.

Un condensatore non permette il passaggio di corrente elettrica, perché il circuito in cui è inserito non ha continuità metallica per la presenza dell’isolante (dielettrico). La continuità, comunque, è presente nelle fasi di carica e di scarica.

Se infatti applichiamo una f.e.m. alle armature, si avrà una tensione fra di esse e quindi si produrrà un campo elettrico, al quale corrisponde la formazione di cariche uguali e contrarie sulle armature stesse. Dunque l’inserimento in circuito di un generatore, ha provocato uno spostamento di elettroni da una armatura all’altra: una corrente elettrica.

Se ora colleghiamo tra loro le due armature, o inseriamo un carico, gli elettroni tenderanno a distribuirsi di nuovo in modo omogeneo. Si avrà cioè un passaggio di corrente, in senso opposto al precedente, che perdurerà fino a quando gli elettroni si sono di nuovo distribuiti uniformemente sulle armature metalliche. Scomparirà così la carica accumulata, e quindi anche la tensione fra le armature ed il campo nel dielettrico: il condensatore è di nuovo scarico.

Se vogliamo analizzare l’andamento della corrente e della tensione di questo transitorio, il problema diventa più complesso. Si può dire che la corrente di carica è alta nell’attimo iniziale del collegamento alla f.e.m.; essa viene soltanto limitata dalla minima resistenza ohmica R dei conduttori esterni e del condensatore. Con l’aumentare della tensione sulle armature del condensatore, la corrente diminuisce progressivamente fino alla carica completa quando il condensatore blocca la corrente.

Nella scarica del condensatore la sua tensione diminuisce nello stesso rapporto della corrente di scarica. Entrambe raggiungono contemporaneamente il valore 0.

Da quanto visto, è chiaro che la carica e la scarica di un condensatore si attuano in un determinato periodo di tempo. Le grandezze intensità di corrente e tensione variano.

La dipendenza dal tempo delle grandezze si nota sull’oscilloscopio.

Come generatore viene utilizzato un generatore a segnali rettangolari. Esso provvede a far sì che la tensione venga costantemente inserita e disinserita.

 

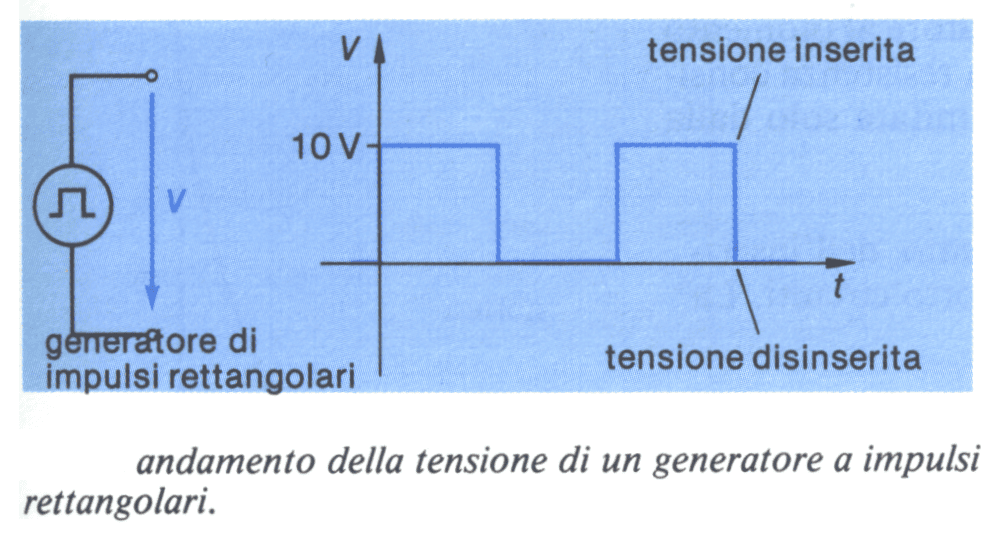
In questo modo si ottengono processi periodici, senza che interruttori debbano essere spostati meccanicamente.

 

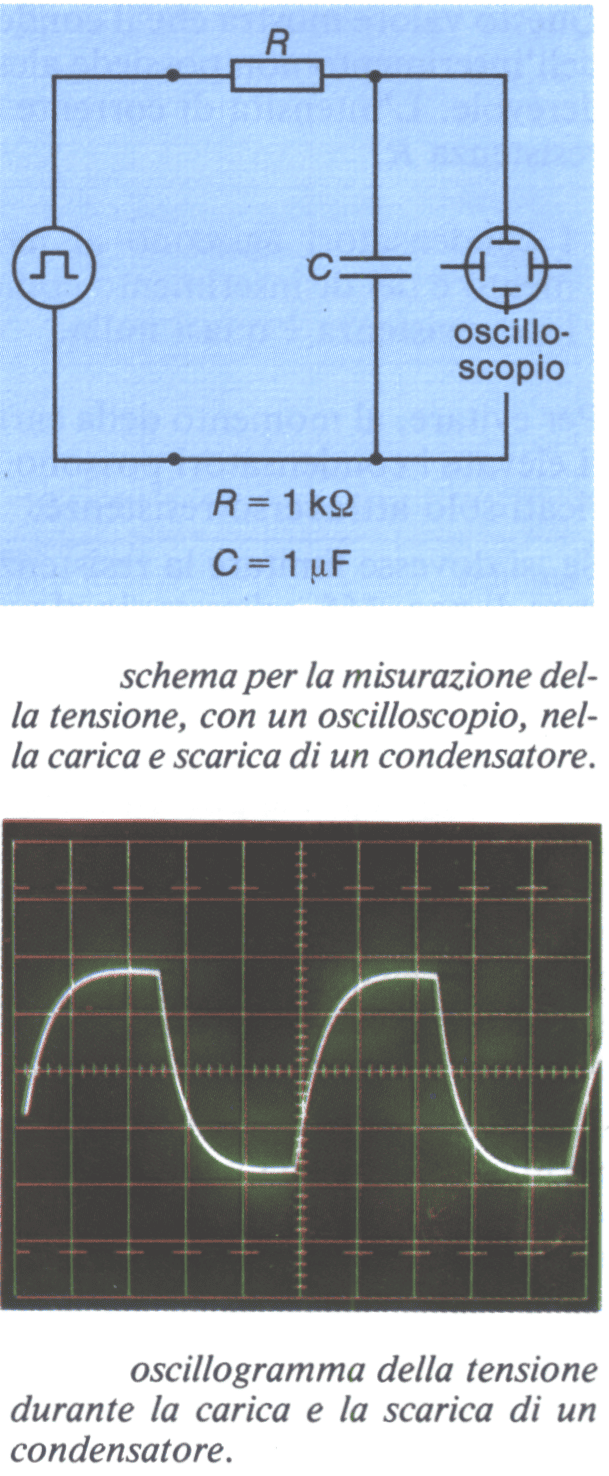
Siccome con un oscilloscopio possono essere riprodotte solo le tensioni, viene misurata la corrente come caduta di tensione sulla resistenza R. L’intensità di corrente può essere calcolata con la relazione:.

Calcolo della corrente massima al momento dell’inserimento:

Tensione del generatore: V = 300 V.

Resistenza: R = 20 kΩ

Caduta di tensione misurata: V = 300 V,

,

Þ Imax = 15 mA

Questo valore mostra che il condensatore al momento dell’inserimento non possiede alcuna resistenza considerevole. L’intensità di corrente è limitata solo dalla resistenza R.

I condensatori agiscono al momento dell’inserimento e del disinserimento come corto circuiti. La loro resistenza è quasi nulla.

Per evitare, al momento della carica e scarica, correnti elevate i condensatori possono essere caricati e scaricati solo attraverso resistenze.

Se si dovesse limitare la resistenza nel circuito, ad esempio al valore di 10 Ω, vi scorrerebbe subito, per breve tempo, una intensità di corrente di 1 A. Questa può portare subito all’interruzione del circuito per fusione del condensatore.

Dalle figure si può chiaramente notare la dipendenza della tensione e dell’intensità di corrente dal tempo. Nella carica, la tensione cresce prima rapidamente e poi più lentamente, finché non si raggiunge il valore del generatore di tensione. Nella scarica, la tensione si abbassa dapprima rapidamente e poi si avvicina a poco a poco alla linea dello zero.

L’intensità di corrente è massima al momento dell’inserimento. Poi cala e tende verso il valore zero quando la tensione è massima (il condensatore è caricato completamente). Nella scarica si inverte la direzione della corrente perché gli elettroni scorrono di nuovo attraverso le armature. La punta massima della corrente di disinserimento è uguale alla punta massima della corrente d’inserimento.

 

 

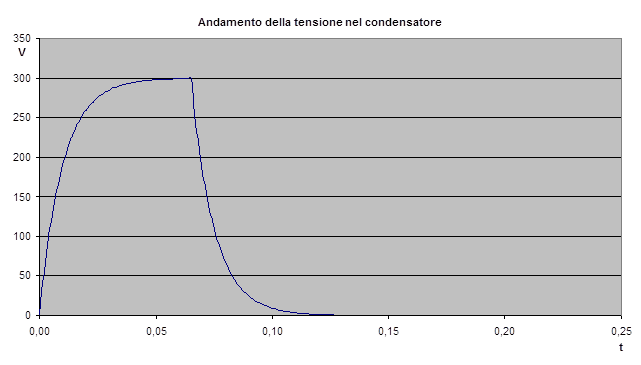
Il tempo per la carica e scarica di un condensatore dipende dalla capacità e dalla resistenza. A capacità più grandi si prolunga il processo di carica. Allo stesso modo si comporta la resistenza: se è grande, l’ostacolo alle cariche sarà grande e il processo di carica durerà più a lungo.

Entrambe queste grandezze vengono riassunte nella costante di tempo τ. Essa ci informa sulla durata dei processi di carica e scarica.

In un tempo t = 1 τ il condensatore è caricato al 63% della sua tensione finale. Nella scarica la sua tensione è diminuita, nel tempo t = 1 τ, al 37% della tensione applicata.

Dopo un tempo t = 5 τ, ogni condensatore può essere considerato completamente carico o completamente scarico.

La costante si ricava tramite la relazione: τ = R·C.

 

⚡ Cos’è la Capacità Elettrica – Guida Introduttiva

La capacità elettrica è una grandezza fisica fondamentale in elettrotecnica, specialmente nello studio dei condensatori. Si tratta della proprietà di un conduttore di accumulare carica elettrica. Vediamo insieme cosa significa, come si calcola e quali sono le formule principali.

📘 Definizione di Capacità Elettrica

La capacità elettrica (C) di un conduttore è definita come il rapporto tra la carica elettrica (Q) accumulata su di esso e il potenziale elettrico (V) al quale è portato.

C = \frac{Q}{V}

📌 L’unità di misura nel Sistema Internazionale è il farad (F), dove:

1, F = \frac{1, C}{1, V}

⚠️ Attenzione: 1 farad è una quantità molto grande. Nella pratica si usano spesso i suoi sottomultipli: microfarad (µF), nanofarad (nF), picofarad (pF).

🧲 Capacità di un Condensatore

Un condensatore è un dispositivo che immagazzina energia elettrica sotto forma di campo elettrico. Il tipo più semplice è il condensatore piano, formato da due armature conduttrici parallele separate da un dielettrico.

Formula della capacità di un condensatore piano:

C = \varepsilon \cdot \frac{S}{d}

Dove:

  • \varepsilon è la costante dielettrica del materiale tra le armature;

  • S è la superficie delle armature;

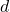  • d è la distanza tra le armature.

📷 [INSERISCI IMMAGINE QUI]
Un disegno schematico di un condensatore piano con le armature, il dielettrico e le grandezze indicate: S, d, ε.

🔌 Collegamenti dei Condensatori

I condensatori possono essere collegati in serie o in parallelo, e in base al tipo di collegamento cambia la capacità equivalente.

Condensatori in serie:

\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}

📷 [INSERISCI IMMAGINE QUI]
Schema di collegamento di condensatori in serie.

Condensatori in parallelo:

C_{eq} = C_1 + C_2 + \cdots + C_n

📷 [INSERISCI IMMAGINE QUI]
Schema di collegamento di condensatori in parallelo.

⚡ Energia immagazzinata in un condensatore

L’energia elettrica immagazzinata in un condensatore carico è data dalla seguente formula:

W = \frac{1}{2} C V^2

📌 Questa energia viene immagazzinata nel campo elettrico generato tra le armature.

🧮 Esempio pratico

Supponiamo di avere un condensatore da 10 μF10 \, \mu F caricato a una tensione di 12 V12 \, V. Qual è la carica immagazzinata?

Q = C \cdot V = 10 \times 10^{-6} \cdot 12 = 120 \times 10^{-6} , C = 120 , \mu C

E l’energia?

W = \frac{1}{2} \cdot 10 \times 10^{-6} \cdot 12^2 = 0.72 , mJ

🧠 Conclusione

La capacità elettrica è una nozione fondamentale per comprendere il comportamento dei circuiti in corrente continua e alternata. Capire come si calcola e come funziona nei condensatori ti aiuterà ad affrontare meglio gli argomenti successivi dell’elettrotecnica.

⚡ Cos’è la Capacità Elettrica – Guida Introduttiva La capacità elettrica è una grandezza fisica fondamentale in elettrotecnica, specialmente nello studio dei condensatori. Si tratta della proprietà di un conduttore di accumulare carica elettrica. Vediamo insieme cosa significa, come si calcola e quali sono le formule principali. 📘 Definizione di Capacità Elettrica La capacità elettrica (C) di un conduttore è definita come il rapporto tra la carica elettrica (Q) accumulata su di esso e il potenziale elettrico (V) al quale è portato. C = \frac{Q}{V} 📌 L’unità di misura nel Sistema Internazionale è il farad (F), dove: 1, F = \frac{1, C}{1, V} ⚠️ Attenzione: 1 farad è una quantità molto grande. Nella pratica si usano spesso i suoi sottomultipli: microfarad (µF), nanofarad (nF), picofarad (pF). 🧲 Capacità di un Condensatore Un condensatore è un dispositivo che immagazzina energia elettrica sotto forma di campo elettrico. Il tipo più semplice è il condensatore piano, formato da due armature conduttrici parallele separate da un dielettrico. Formula della capacità di un condensatore piano: C = \varepsilon \cdot \frac{S}{d} Dove: \varepsilon è la costante dielettrica del materiale tra le armature; S è la superficie delle armature; d è la distanza tra le armature. 📷 [INSERISCI IMMAGINE QUI] Un disegno schematico di un condensatore piano con le armature, il dielettrico e le grandezze indicate: S, d, ε. 🔌 Collegamenti dei Condensatori I condensatori possono essere collegati in serie o in parallelo, e in base al tipo di collegamento cambia la capacità equivalente. Condensatori in serie: \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n} 📷 [INSERISCI IMMAGINE QUI] Schema di collegamento di condensatori in serie. Condensatori in parallelo: C_{eq} = C_1 + C_2 + \cdots + C_n 📷 [INSERISCI IMMAGINE QUI] Schema di collegamento di condensatori in parallelo. ⚡ Energia immagazzinata in un condensatore L’energia elettrica immagazzinata in un condensatore carico è data dalla seguente formula: W = \frac{1}{2} C V^2 📌 Questa energia viene immagazzinata nel campo elettrico generato tra le armature. 🧮 Esempio pratico Supponiamo di avere un condensatore da 10   𝜇 𝐹 10μF caricato a una tensione di 12   𝑉 12V. Qual è la carica immagazzinata? Q = C \cdot V = 10 \times 10^{-6} \cdot 12 = 120 \times 10^{-6} , C = 120 , \mu C E l’energia? W = \frac{1}{2} \cdot 10 \times 10^{-6} \cdot 12^2 = 0.72 , mJ 🧠 Conclusione La capacità elettrica è una nozione fondamentale per comprendere il comportamento dei circuiti in corrente continua e alternata. Capire come si calcola e come funziona nei condensatori ti aiuterà ad affrontare meglio gli argomenti successivi dell’elettrotecnica.

⚡ Cos’è la Capacità Elettrica – Guida Introduttiva La capacità elettrica è una grandezza fisica fondamentale in elettrotecnica, specialmente nello studio dei condensatori. Si tratta della proprietà di un conduttore di accumulare carica elettrica. Vediamo insieme cosa significa, come si calcola e quali sono le formule principali. 📘 Definizione di Capacità Elettrica La capacità elettrica (C) di un conduttore è definita come il rapporto tra la carica elettrica (Q) accumulata su di esso e il potenziale elettrico (V) al quale è portato. C = \frac{Q}{V} 📌 L’unità di misura nel Sistema Internazionale è il farad (F), dove: 1, F = \frac{1, C}{1, V} ⚠️ Attenzione: 1 farad è una quantità molto grande. Nella pratica si usano spesso i suoi sottomultipli: microfarad (µF), nanofarad (nF), picofarad (pF). 🧲 Capacità di un Condensatore Un condensatore è un dispositivo che immagazzina energia elettrica sotto forma di campo elettrico. Il tipo più semplice è il condensatore piano, formato da due armature conduttrici parallele separate da un dielettrico. Formula della capacità di un condensatore piano: C = \varepsilon \cdot \frac{S}{d} Dove: \varepsilon è la costante dielettrica del materiale tra le armature; S è la superficie delle armature; d è la distanza tra le armature. 📷 [INSERISCI IMMAGINE QUI] Un disegno schematico di un condensatore piano con le armature, il dielettrico e le grandezze indicate: S, d, ε. 🔌 Collegamenti dei Condensatori I condensatori possono essere collegati in serie o in parallelo, e in base al tipo di collegamento cambia la capacità equivalente. Condensatori in serie: \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n} 📷 [INSERISCI IMMAGINE QUI] Schema di collegamento di condensatori in serie. Condensatori in parallelo: C_{eq} = C_1 + C_2 + \cdots + C_n 📷 [INSERISCI IMMAGINE QUI] Schema di collegamento di condensatori in parallelo. ⚡ Energia immagazzinata in un condensatore L’energia elettrica immagazzinata in un condensatore carico è data dalla seguente formula: W = \frac{1}{2} C V^2 📌 Questa energia viene immagazzinata nel campo elettrico generato tra le armature. 🧮 Esempio pratico Supponiamo di avere un condensatore da 10   𝜇 𝐹 10μF caricato a una tensione di 12   𝑉 12V. Qual è la carica immagazzinata? Q = C \cdot V = 10 \times 10^{-6} \cdot 12 = 120 \times 10^{-6} , C = 120 , \mu C E l’energia? W = \frac{1}{2} \cdot 10 \times 10^{-6} \cdot 12^2 = 0.72 , mJ 🧠 Conclusione La capacità elettrica è una nozione fondamentale per comprendere il comportamento dei circuiti in corrente continua e alternata. Capire come si calcola e come funziona nei condensatori ti aiuterà ad affrontare meglio gli argomenti successivi dell’elettrotecnica. 📘 Capacità di un Condensatore Cilindrico Consideriamo un condensatore cilindrico costituito da due cilindri coassiali di lunghezza 𝑙 l, uno interno conduttore di raggio 𝑎 a, l’altro conduttore cavo di raggio 𝑏 b, separati da un dielettrico. 📷 [INSERISCI IMMAGINE – sezione cilindrica con raggio a e b] Sia 𝑄 Q la carica elettrica positiva sul cilindro interno, e − 𝑄 −Q quella sul cilindro esterno. Applichiamo la legge di Gauss: \oint \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_0} Nel caso specifico di simmetria cilindrica: E \cdot 2\pi r l = \frac{Q}{\varepsilon_0} Da cui: E(r) = \frac{Q}{2\pi \varepsilon_0 l r} Per determinare la differenza di potenziale tra le armature (tra 𝑎 a e 𝑏 b): V = -\int_a^b \vec{E} \cdot d\vec{l} = - \int_a^b \frac{Q}{2\pi \varepsilon_0 l r} dr = \frac{Q}{2\pi \varepsilon_0 l} \ln{\left( \frac{b}{a} \right)} Dalla relazione: C = \frac{Q}{V} si ottiene la capacità del condensatore cilindrico: C = \frac{2\pi \varepsilon_0 l}{\ln(b/a)} 🌐 Capacità di un Condensatore Sferico Consideriamo ora un condensatore sferico costituito da due sfere concentriche, una interna di raggio 𝑎 a, e una esterna cava di raggio 𝑏 b. 📷 [INSERISCI IMMAGINE – sezione sferica con raggi a e b] La carica 𝑄 Q si trova sulla sfera interna, e − 𝑄 −Q sulla sfera esterna. Utilizzando nuovamente la legge di Gauss: \oint \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_0} Otteniamo il campo elettrico: E(r) = \frac{Q}{4\pi \varepsilon_0 r^2} Per il potenziale tra le due sfere: V = -\int_a^b \vec{E} \cdot d\vec{l} = - \int_a^b \frac{Q}{4\pi \varepsilon_0 r^2} dr = \frac{Q}{4\pi \varepsilon_0} \left( \frac{1}{a} - \frac{1}{b} \right) Quindi: C = \frac{Q}{V} = 4\pi \varepsilon_0 \cdot \frac{ab}{b - a} ⚡ Energia immagazzinata da un condensatore L’energia potenziale immagazzinata in un condensatore è data da: U = \frac{1}{2} C V^2 oppure, in funzione della carica: U = \frac{Q^2}{2C} 🔁 Espressione generale dell’energia in un campo elettrostatico L’energia immagazzinata in un campo elettrostatico si può anche esprimere come: U = \int_{\text{volume}} \frac{1}{2} \varepsilon_0 E^2 , dV 📌 Questa formula è utile nel calcolo dell’energia in configurazioni complesse. ✅ Conclusioni Abbiamo visto come si calcolano la capacità e l’energia immagazzinata in condensatori con geometrie più avanzate, come quelli cilindrici e sferici. Questi concetti sono fondamentali in elettrotecnica e fisica applicata, specialmente in sistemi ad alta tensione o in geometrie non planari.

📘 Capacità di un Condensatore Cilindrico Consideriamo un condensatore cilindrico costituito da due cilindri coassiali di lunghezza 𝑙 l, uno interno conduttore di raggio 𝑎 a, l’altro conduttore cavo di raggio 𝑏 b, separati da un dielettrico. 📷 [INSERISCI IMMAGINE – sezione cilindrica con raggio a e b] Sia 𝑄 Q la carica elettrica positiva sul cilindro interno, e − 𝑄 −Q quella sul cilindro esterno. Applichiamo la legge di Gauss: \oint \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_0} Nel caso specifico di simmetria cilindrica: E \cdot 2\pi r l = \frac{Q}{\varepsilon_0} Da cui: E(r) = \frac{Q}{2\pi \varepsilon_0 l r} Per determinare la differenza di potenziale tra le armature (tra 𝑎 a e 𝑏 b): V = -\int_a^b \vec{E} \cdot d\vec{l} = - \int_a^b \frac{Q}{2\pi \varepsilon_0 l r} dr = \frac{Q}{2\pi \varepsilon_0 l} \ln{\left( \frac{b}{a} \right)} Dalla relazione: C = \frac{Q}{V} si ottiene la capacità del condensatore cilindrico: C = \frac{2\pi \varepsilon_0 l}{\ln(b/a)} 🌐 Capacità di un Condensatore Sferico Consideriamo ora un condensatore sferico costituito da due sfere concentriche, una interna di raggio 𝑎 a, e una esterna cava di raggio 𝑏 b. 📷 [INSERISCI IMMAGINE – sezione sferica con raggi a e b] La carica 𝑄 Q si trova sulla sfera interna, e − 𝑄 −Q sulla sfera esterna. Utilizzando nuovamente la legge di Gauss: \oint \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_0} Otteniamo il campo elettrico: E(r) = \frac{Q}{4\pi \varepsilon_0 r^2} Per il potenziale tra le due sfere: V = -\int_a^b \vec{E} \cdot d\vec{l} = - \int_a^b \frac{Q}{4\pi \varepsilon_0 r^2} dr = \frac{Q}{4\pi \varepsilon_0} \left( \frac{1}{a} - \frac{1}{b} \right) Quindi: C = \frac{Q}{V} = 4\pi \varepsilon_0 \cdot \frac{ab}{b - a} ⚡ Energia immagazzinata da un condensatore L’energia potenziale immagazzinata in un condensatore è data da: U = \frac{1}{2} C V^2 oppure, in funzione della carica: U = \frac{Q^2}{2C} 🔁 Espressione generale dell’energia in un campo elettrostatico L’energia immagazzinata in un campo elettrostatico si può anche esprimere come: U = \int_{\text{volume}} \frac{1}{2} \varepsilon_0 E^2 , dV 📌 Questa formula è utile nel calcolo dell’energia in configurazioni complesse. ✅ Conclusioni Abbiamo visto come si calcolano la capacità e l’energia immagazzinata in condensatori con geometrie più avanzate, come quelli cilindrici e sferici. Questi concetti sono fondamentali in elettrotecnica e fisica applicata, specialmente in sistemi ad alta tensione o in geometrie non planari.

Capacità cilindrica. Condensatore cilindrico

Consideriamo un sistema costituito da due conduttori cilindrici di lunghezza \( L \), uno interno conduttore di raggio \( a \) e l’altro cilindro coassiale di raggio \( b \), con \( b > a \).

Q è la carica elettrica sull’armatura interna (positiva), –Q quella su quella esterna.

Configurazione:

Condensatore cilindrico

Con simmetria cilindrica, possiamo considerare cilindri di raggio \( r \) e lunghezza \( L \), con carica distribuita uniformemente sulla superficie interna.

Dalla legge di Gauss:

\oint \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_0} \Rightarrow E \cdot 2\pi r L = \frac{Q}{\varepsilon_0}

Da cui:

E = \frac{Q}{2 \pi \varepsilon_0 r L}

Per la definizione di potenziale e considerando la simmetria cilindrica:

V = - \int_a^b \vec{E} \cdot d\vec{l} = - \int_a^b \frac{Q}{2 \pi \varepsilon_0 r L} dr = - \frac{Q}{2 \pi \varepsilon_0 L} \ln \left( \frac{b}{a} \right)

Dalla relazione \( C = \frac{Q}{V} \), risulta:

C = \frac{2 \pi \varepsilon_0 L}{\ln (b/a)}

Condensatore sferico

Consideriamo due sfere conduttrici concentriche di raggio \( a \) e \( b \) (con \( b > a \)) e lunghezza infinita, la sfera interna ha carica \( Q \), l’altra –Q.

Per simmetria, il campo elettrico tra le sfere dipende solo da \( r \):

\oint \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_0} \Rightarrow E \cdot 4\pi r^2 = \frac{Q}{\varepsilon_0}

Risolvendo:

E = \frac{Q}{4 \pi \varepsilon_0 r^2}

Integrando per trovare la differenza di potenziale tra \( a \) e \( b \):

V = - \int_a^b \frac{Q}{4 \pi \varepsilon_0 r^2} dr = \frac{Q}{4 \pi \varepsilon_0} \left( \frac{1}{a} - \frac{1}{b} \right)

Quindi:

C = \frac{Q}{V} = \frac{4 \pi \varepsilon_0}{\frac{1}{a} - \frac{1}{b}}

Energia immagazzinata in un condensatore

Dalla definizione di potenziale, il lavoro necessario per caricare un condensatore da 0 a Q è:

W = \int_0^Q V dq = \int_0^Q \frac{q}{C} dq = \frac{Q^2}{2C}

Ma vale anche:

W = \frac{1}{2} C V^2 = \frac{1}{2} Q V

Energia immagazzinata in un campo elettrostatico

Nota come questa energia è contenuta nel campo elettrico. Possiamo esprimerla in funzione del campo, integrando sull’intero volume:

U = \frac{\varepsilon_0}{2} \int E^2 dV

Nel caso di simmetria sferica (come nel condensatore sferico), con:

E = \frac{Q}{4\pi \varepsilon_0 r^2}

Risulta:

U = \frac{\varepsilon_0}{2} \int_a^b \left( \frac{Q}{4\pi \varepsilon_0 r^2} \right)^2 4\pi r^2 dr = \frac{Q^2}{8\pi \varepsilon_0} \left( \frac{1}{a} - \frac{1}{b} \right)

Che coincide con l’espressione precedente dell’energia potenziale elettrica.

Infine, possiamo riscrivere l’energia potenziale elettrica anche come:

U = \frac{1}{2} \int \rho(\vec{r}) V(\vec{r}) d^3 r

— **Nota**: Sostituisci `URL_DELL_IMMAGINE` con il vero URL dell’immagine caricata nella tua libreria media WordPress (es: `https://www.tuosito.it/wp-content/uploads/2025/04/34f39f40.png`). Vuoi che ti generi anche il file `.html` oppure direttamente il plugin WordPress con questo contenuto come shortcode?

Articoli correlati

01-Il Campo Elettrico

03-Collegamenti di condensatori

Let’s Create Your Own Event Group.

Blog di Megistone

Megistone - Per non perdere l'orientamento

Proudly powered by WordPress | Tema: Newsup di Themeansar.