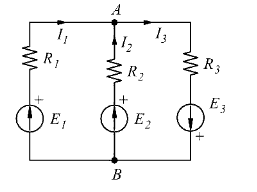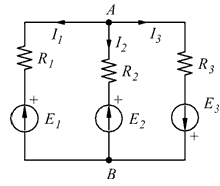
Applicando la formula:
![]()
avremo:
![]()
Studio del ramo 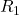 con Kirchhoff
con Kirchhoff
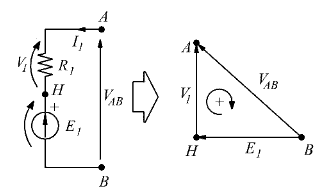
![]()
![]()
![]()
![]()
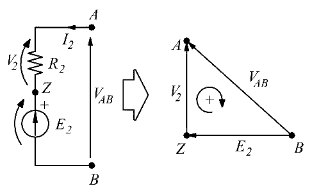
Studio del ramo 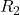 con Kirchhoff
con Kirchhoff
![]()
![]()
![]()
![]()
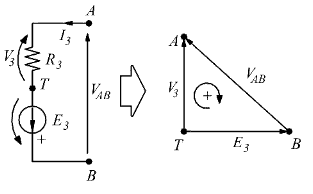
Studio del ramo 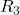 con Kirchhoff
con Kirchhoff
![]()
![]()
![]()
![]()
Il senso effettivo delle tre correnti nel circuito è indicato in figura. Esse valgono rispettivamente:
![]()
![]()
![]()