Dati
Legge di Kirchhoff sulla maglia
![]()
![]()
Espressione con la corrente 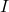
![]()
![]()
Calcolo di 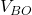
![]()
Condizione per 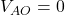
Affinché ![]() , la corrente deve soddisfare:
, la corrente deve soddisfare:
![]()
![]()
Verifica finale
![]()
Quindi la condizione è soddisfatta: ![]()
Megistone - Per non perdere l'orientamento
![]()
![]()
![]()
![]()
![]()
Affinché ![]() , la corrente deve soddisfare:
, la corrente deve soddisfare:
![]()
![]()
![]()
Quindi la condizione è soddisfatta: ![]()