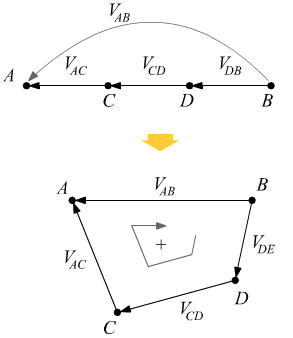
Risoluzione di un circuito con il metodo delle maglie
Dati del circuito
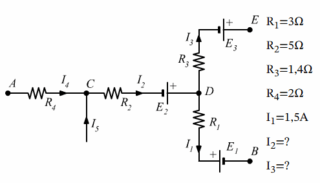
Risoluzione del circuito con le leggi di Kirchhoff
Dati noti
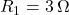
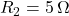
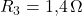
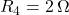
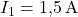
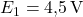 ,
, 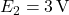 ,
, 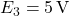
Obiettivo
Determinare le correnti ![]() e
e ![]() .
.
Applicazione della prima legge di Kirchhoff (nodo D)
![]()
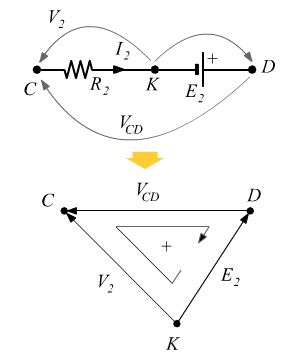
Tratto CD
![]()
![]()
Calcolo di 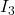
Essendo ![]() , si ha:
, si ha:
![]()
per la legge di Ohm abbiamo:
![]()
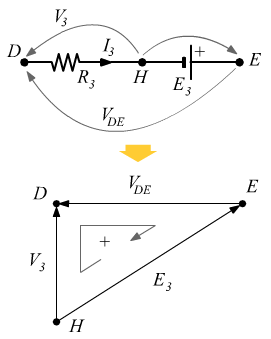
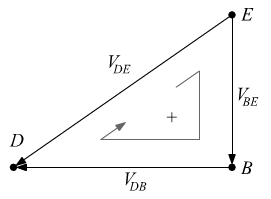
Tratto DE – Maglia con 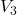 e
e 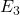
![]()
![]()
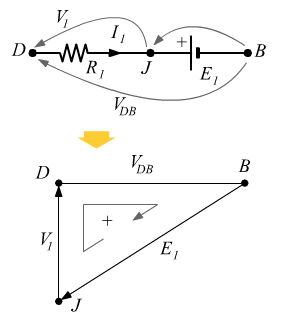
Tratto DB
![]()
![]()
Calcolo della tensione 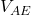
![]()
Verifica con legge di Kirchhoff
![]()
Equazione della maglia: si verifica la coerenza con il segno e la somma algebrica delle tensioni.
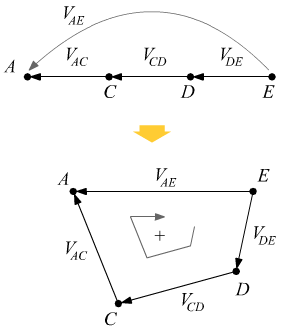
Tratto BA
![]()
Da cui si può calcolare ![]() come somma algebrica delle tensioni note nei tratti intermedi.
come somma algebrica delle tensioni note nei tratti intermedi.
Calcolo di 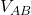
![]()
Da cui:
![]()
Calcolo della tensione 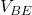
Scriviamo l’equazione di maglia:
![]()
![]()