Variazione di tensione e densità di energia in un condensatore con dielettrico inserito
Un condensatore tra le cui armature è stato fatto il vuoto è connesso ad una batteria da 12 V e caricato. In seguito viene scollegato dalla batteria tra le sue armature e inserito un materiale di costante dielettrica ![]() .
.
Calcola la variazione della differenza di potenziale tra le sue armature fra quando era connesso alla batteria e quando è inserito completamente il materiale. Le armature sono distanti tra loro 3 mm, quanto vale la densità volumica di energia finale?
Soluzione
1) Nuova tensione con dielettrico
Dalla relazione ![]() e
e ![]() , la capacità del condensatore diventa 3,5 volte più grande.
, la capacità del condensatore diventa 3,5 volte più grande.
Quindi la tensione si riduce di 3,5 volte:
![]()
2) Variazione di differenza di potenziale
![]()
3) Equazione con capacità iniziale e finale
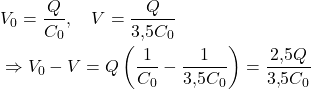
4) Relazione tra superficie e capacità
![]()
5) Densità di energia volumica
![]()
![]()