Analisi del campo elettrico e del potenziale in un condensatore piano
Un condensatore ad armature piane parallele, immerse nel vuoto, distanti di ![]() , presenta una capacità
, presenta una capacità ![]() ed è sottoposto ad una certa tensione. Assumendo sulle armature una carica
ed è sottoposto ad una certa tensione. Assumendo sulle armature una carica ![]() , trovare:
, trovare:
- Il valore della tensione applicata.
- Il valore del campo elettrico
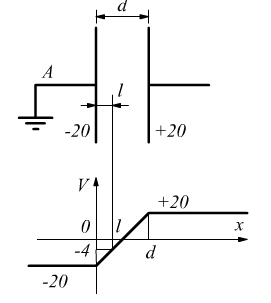
 e l’andamento della tensione dentro il condensatore.
e l’andamento della tensione dentro il condensatore. - Il valore della tensione in un punto interno al condensatore distante
 dall’armatura negativa (cioè a potenziale minore).
dall’armatura negativa (cioè a potenziale minore). - Come al punto 3) ipotizzando che l’armatura negativa venga messa a massa.
Soluzione
1) Calcolo della tensione tra le armature
![]()
2) Campo elettrico uniforme
![]()
L’andamento del potenziale all’interno del condensatore è lineare: parte da \(-20 \, \text{V}\) sull’armatura A e arriva a \(+20 \, \text{V}\) sull’armatura B.
La relazione è: ![]()
3) Potenziale ad una distanza di 2 mm dall’armatura negativa
Dato: ![]()
![]()
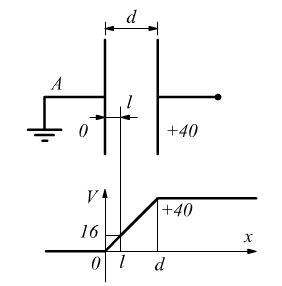
4) Potenziale con armatura negativa a massa
Se \( V_A = 0 \), allora:
![]()