Esercizio 2: Soluzione

Condensatore piano: calcolo della carica con e senza dielettrico

Un condensatore piano le cui armature hanno un’area:

$S = 4 \text{dm}^2 = 4 \cdot 10^{-2} \text{m}^2$

e sono poste ad una distanza:

$d = 2 \text{mm} = 2 \cdot 10^{-3} \text{m}$

viene caricato ad una tensione:

$V = 100 \text{V}$

Problema

Quanto vale la carica accumulata nel vuoto?
Quanto vale la carica se viene interposto un dielettrico con costante dielettrica relativa $\varepsilon_r = 2$ ?

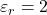Soluzione

1. Caso senza dielettrico (nel vuoto)

La capacità si calcola con:

$C = \varepsilon_0 \cdot \frac{S}{d} = 8.85 \cdot 10^{-12} \cdot \frac{4 \cdot 10^{-2}}{2 \cdot 10^{-3}} = 1.77 \cdot 10^{-10} \text{F}$

Calcoliamo la carica accumulata:

$Q = C \cdot V = 1.77 \cdot 10^{-10} \cdot 100 = 1.77 \cdot 10^{-8} \text{C}$

2. Caso con dielettrico 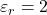$\varepsilon_r = 2$

La capacità raddoppia:

$C' = \varepsilon_r \cdot C = 2 \cdot 1.77 \cdot 10^{-10} = 3.54 \cdot 10^{-10} \text{F}$

E quindi anche la carica raddoppia:

$Q' = C' \cdot V = 3.54 \cdot 10^{-10} \cdot 100 = 3.54 \cdot 10^{-8} \text{C}$

Risultati finali

Carica nel vuoto: $Q = 1.77 \cdot 10^{-8} \text{C}$
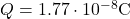
Carica con dielettrico: $Q' = 3.54 \cdot 10^{-8} \text{C}$

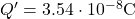
Questo esempio mostra chiaramente come l’introduzione di un materiale dielettrico aumenti la capacità del condensatore e, di conseguenza, la quantità di carica che può immagazzinare a parità di tensione.

Condensatore piano: calcolo della carica con e senza dielettrico

Problema

Soluzione

1. Caso senza dielettrico (nel vuoto)

2. Caso con dielettrico $\varepsilon_r = 2$

Risultati finali

Articoli correlati

Esercizio 20: Soluzione

Esercizio 19: Soluzione

Esercizio 18: Soluzione