Esercizio 11: Soluzione

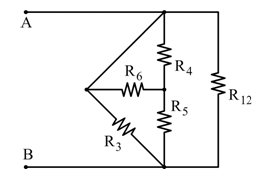
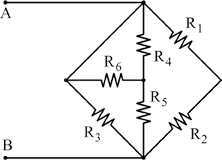
In questo esercizio analizziamo una rete resistiva con combinazioni in serie e parallelo. Il primo passo è osservare che le resistenze R₁ e R₂ sono in serie:

$R_{12} = R_1 + R_2 = 50 + 30 = 80\,\Omega$

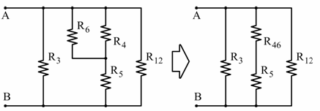
A questo punto riconosciamo che R₄ e R₆ sono in parallelo, e possono essere sostituite con una resistenza equivalente R₄₆:

$R_{46} = \frac{R_4 \cdot R_6}{R_4 + R_6} = \frac{40 \cdot 10}{50} = 8\,k\Omega$

Il circuito può quindi essere riscritto come un parallelo di tre rami: R₃, R₄₆+R₅, R₁₂.

L’inverso della resistenza equivalente è dato dalla somma delle conduttanze:

$\frac{1}{R_{AB}} = \frac{1}{R_3} + \frac{1}{R_{46} + R_5} + \frac{1}{R_{12}}$

Inserendo i valori numerici:

$\frac{1}{R_{AB}} = \frac{1}{50} + \frac{1}{17 + 8} + \frac{1}{80} = 0{,}0725\,S$

Da cui:

$R_{AB} = \frac{1}{0{,}0725} = 13{,}8\,\Omega$

Conclusione

Attraverso un’attenta semplificazione del circuito combinato, è possibile ridurre la rete resistiva a un parallelo di tre rami. L’utilizzo di formule per combinazioni in serie e parallelo risulta fondamentale per arrivare alla resistenza equivalente.

Conclusione

Articoli correlati

Esercizio 12: Soluzione

Esercizio 9: Soluzione

Esercizio 8: Soluzione