Esercizio 10: Soluzione

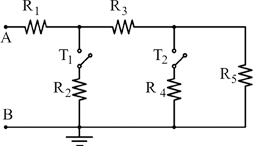
Analizziamo quattro configurazioni diverse dei deviatori T₁ e T₂ per determinare la resistenza equivalente R_AB in ciascun caso.

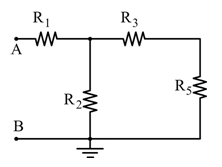
🔹 Caso A – T₁ aperto, T₂ chiuso

Si ha il seguente schema:

Esercizio 10 - Caso A

La formula della resistenza equivalente è:

$R_{AB} = R_1 + R_3 + \frac{R_4 \cdot R_5}{R_4 + R_5}$

Sostituendo i valori:

$R_{AB} = 2{,}7 + 0{,}4 + \frac{1 \cdot 6}{1 + 6} = 3{,}95\,k\Omega$

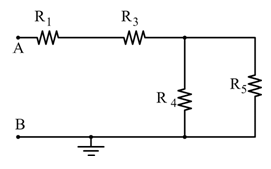
🔹 Caso B – T₁ chiuso, T₂ aperto

In questo caso R₄ è esclusa:

Esercizio 10 - Caso B

La formula diventa:

$R_{AB} = R_1 + \frac{R_2 \cdot (R_3 + R_5)}{R_2 + R_3 + R_5}$

Con i valori:

$R_{AB} = 2{,}7 + \frac{8 \cdot 1{,}4}{9{,}4} = 3{,}89\,k\Omega$

🔹 Caso C – T₁ e T₂ chiusi

Nessuna resistenza è esclusa:

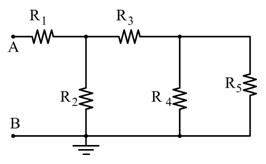
Esercizio 10 - Caso C

Applicando la formula completa:

$R_{AB} = R_1 + \frac{R_2 \cdot [R_3 + (R_4 \cdot R_5 / (R_4 + R_5))]}{R_2 + R_3 + (R_4 \cdot R_5 / (R_4 + R_5))}$

Con i valori:

$R_{AB} = 2{,}7 + \frac{8 \cdot 1{,}25}{9{,}25} = 3{,}78\,k\Omega$

🔹 Caso D – T₁ e T₂ aperti

Le resistenze R₂ e R₄ sono escluse:

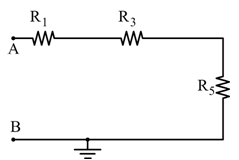
La formula è semplicemente:

$R_{AB} = R_1 + R_3 + R_5 = 2{,}7 + 0{,}4 + 1 = 4{,}1\,k\Omega$

Conclusione

Questo esercizio mostra l’importanza della configurazione dei deviatori nella determinazione della resistenza equivalente. Le variazioni topologiche nei circuiti influiscono significativamente sul valore di R_AB.

🔹 Caso A – T₁ aperto, T₂ chiuso

🔹 Caso B – T₁ chiuso, T₂ aperto

🔹 Caso C – T₁ e T₂ chiusi

🔹 Caso D – T₁ e T₂ aperti

Conclusione

Articoli correlati

Esercizio 6: Soluzione

Esercizio 5: Soluzione

Collegamento di resistenze : esercizi risolti

Esercizio 10: Soluzione

🔹 Caso A – T1 aperto, T2 chiuso

🔹 Caso B – T1 chiuso, T2 aperto

🔹 Caso C – T1 e T2 chiusi

🔹 Caso D – T1 e T2 aperti

Conclusione

Articoli correlati

Esercizio 6: Soluzione

Esercizio 5: Soluzione

Collegamento di resistenze : esercizi risolti

🔹 Caso A – T₁ aperto, T₂ chiuso

🔹 Caso B – T₁ chiuso, T₂ aperto

🔹 Caso C – T₁ e T₂ chiusi

🔹 Caso D – T₁ e T₂ aperti