Esercizio 9: Soluzione

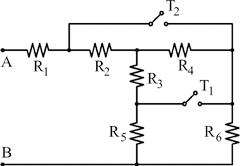
In questo esercizio si analizzano quattro casi diversi di configurazioni resistive. Per ciascun caso, si calcola la resistenza equivalente tra i punti A e B.

🔹 Caso A

Nel primo caso, riconosciamo una configurazione in cui possiamo applicare la seguente formula:

$R_{AB} = (R_1 + R_2) + \frac{(R_3 + R_5) \cdot (R_4 + R_6)}{(R_3 + R_5) + (R_4 + R_6)}$

Sostituendo i valori:

$R_{AB} = (50 + 50) + \frac{300 \cdot 300}{300 + 300} = 100 + 150 = 250\Omega$

Schema:

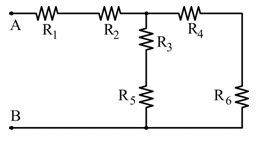
Esercizio 9 - Caso A

🔹 Caso B

Qui si ha una combinazione più articolata, che richiede l’uso della resistenza equivalente di più gruppi:

$R_{AB} = R_1 + \left\{ R_6 \parallel \left[ \left( R_2 \parallel R_4 \right) + R_3 + R_5 \right] \right\}$

Sostituendo i valori:

$R_{AB} = 50 + 100 \bigg/ \left[ \frac{50 \cdot 200}{250} + 200 + 100 \right] = 50 + \frac{100 \cdot 340}{440} = 50 + 77.27 = 127.27\Omega$

Schema:

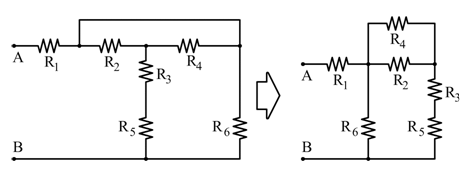
Esercizio 9 - Caso B

🔹 Caso C

La configurazione è una serie mista con paralleli:

$R_{AB} = R_1 + R_2 + \left( R_3 \parallel R_4 \right) + \left( R_5 \parallel R_6 \right)$

$R_{AB} = 50 + 50 + \frac{200 \cdot 200}{200 + 200} + \frac{100 \cdot 100}{100 + 100} = 100 + 100 + 50 = 250\Omega$

Schema:

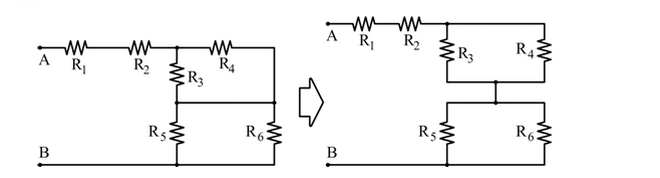
Esercizio 9 - Caso C

🔹 Caso D

Con entrambi i deviatori chiusi, la configurazione si semplifica notevolmente:

$R_{AB} = R_1 + R_{56} = 50 + \frac{100 \cdot 100}{100 + 100} = 50 + 50 = 100\Omega$

Schema:

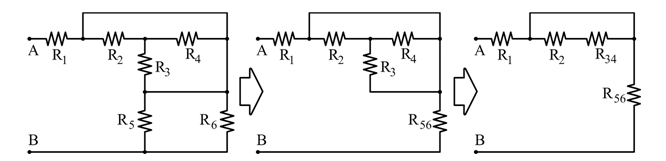
Esercizio 9 - Caso D

Conclusioni

L’esercizio mostra come semplificare circuiti resistivi complessi mediante riduzioni successive di serie e paralleli. È fondamentale identificare i blocchi equivalenti per facilitare il calcolo della resistenza totale.

🔹 Caso A

🔹 Caso B

🔹 Caso C

🔹 Caso D

Conclusioni

Articoli correlati

Esercizio 12: Soluzione

Esercizio 11: Soluzione

Esercizio 8: Soluzione