Con il tasto T chiuso si ha:
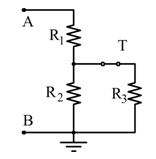
![]()
Nel nostro caso ![]() , per cui si imposta il sistema:
, per cui si imposta il sistema:

Proseguendo sulla prima equazione:
![]()
Moltiplichiamo ambo i membri per ![]() :
:
![]()
Sviluppando:
![]()
Applicando la formula risolutiva del trinomio di secondo grado:
![]()
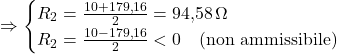
Infine:
![]()
Megistone - Per non perdere l'orientamento
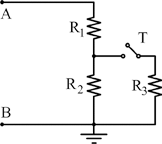
Con il tasto T chiuso si ha:

![]()
Nel nostro caso ![]() , per cui si imposta il sistema:
, per cui si imposta il sistema:

Proseguendo sulla prima equazione:
![]()
Moltiplichiamo ambo i membri per ![]() :
:
![]()
Sviluppando:
![]()
Applicando la formula risolutiva del trinomio di secondo grado:
![]()
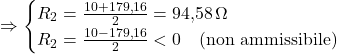
Infine:
![]()