Esercizio 7: Soluzione

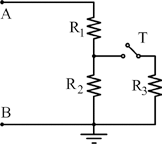
Nel caso il tasto T sia aperto, la resistenza R₃ è esclusa dal circuito e per andare dal nodo A al nodo B dobbiamo attraversare prima R₁ e poi R₂. Pertanto, R_AB è la serie di R₁ con R₂:

$R_{AB} = R_1 + R_2 = 80 + 20 = 100\,\Omega$

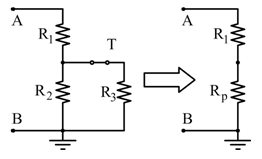
Nel caso il tasto T sia chiuso, R₂ e R₃ sono in parallelo. Si calcola la resistenza equivalente R_p:

$R_p = R_2 \parallel R_3 = \frac{20 \cdot 2000}{2020} = 19{,}80\,\Omega$

Trovandosi R₁ in serie con R_p:

$R_{AB} = R_1 + R_p = 80 + 19{,}8 = 99{,}8\,\Omega$

Ora si vuole trovare il valore della R_x da sostituire a R₃ affinché R_AB = 96 Ω (con tasto chiuso). Poiché con tasto aperto R_AB rimane 100 Ω, analizziamo il caso a tasto chiuso:

$R_{AB} = R_1 + \frac{R_2 \cdot R_x}{R_2 + R_x} \Rightarrow 96 = 80 + \frac{20 \cdot R_x}{20 + R_x}$

$16 = \frac{20 \cdot R_x}{20 + R_x}$

Il problema diventa algebrico:

$(20 + R_x) \cdot 16 = 20 \cdot R_x \Rightarrow 320 + 16 R_x = 20 R_x \Rightarrow 320 = 4 R_x$

$R_x = \frac{320}{4} = 80\,\Omega$

Articoli correlati

Esercizio 12: Soluzione

Esercizio 11: Soluzione

Esercizio 9: Soluzione