Dato che le tre resistenze sono in parallelo, deve valere la relazione:
![]()
![]()
Ora, ammettendo che ![]() ed
ed ![]() mantenendo
mantenendo ![]() , troviamo
, troviamo ![]() :
:
![]()
![]()
Megistone - Per non perdere l'orientamento
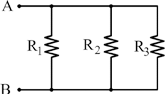
Dato che le tre resistenze sono in parallelo, deve valere la relazione:
![]()
![]()
Ora, ammettendo che ![]() ed
ed ![]() mantenendo
mantenendo ![]() , troviamo
, troviamo ![]() :
:
![]()
![]()