🧮 Esercizi sulle Disposizioni
🔹 Esercizio 12 – Numeri di 5 cifre con restrizioni
Domanda: Quanti numeri di 5 cifre, con o senza ripetizioni, si possono formare con le 10 cifre del sistema decimale senza che la prima cifra sia 0?
L’insieme delle cifre è A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
-
Con ripetizione ammessa:
La prima cifra può essere scelta tra 1 e 9 (quindi 9 scelte), e le restanti 4 cifre tra tutte e 10:
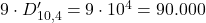
-
Con cifre tutte diverse:
La prima cifra può essere scelta tra 1 e 9 (9 scelte), e le successive 4 tra le rimanenti 9 cifre (escludendo la prima):
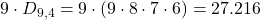
📌 Risultato:
- Con ripetizione: 90.000 numeri
- Senza ripetizione: 27.216 numeri