Grandezze fisiche

La fisica rappresenta il laboratorio naturale per l’applicazione del metodo scientifico: esperimento, con osservazione quantitativamente accurata dei dati; astrazione e formulazione di una legge in forma matematica; previsione di nuovi risultati.

La fisica è una scienza quantitativa. Al di là di una semplice descrizione, essa mira a stabilire la relazione che corre tra le grandezze (grandezze fisiche) che definiscono il fenomeno. I risultati delle osservazioni sperimentali e le previsioni delle teorie sono sempre riconducibili a numeri: perciò il linguaggio usato nella fisica è il linguaggio matematico che, con una scrittura simbolica breve (formula), permette di abbracciare tutta la legge.

Per descrivere la caduta di un corpo, una persona priva di conoscenze nel campo della fisica dice che il corpo, prima fermo, ha preso cadere sempre più in fretta: l’idea del processo risulta, in tal modo, vaga e approssimata. Se invece diciamo, utilizzando il linguaggio della scienza che il corpo parte dallo stato di riposo e cade con accelerazione costante di 9,8 m/sec², ci rendiamo subito conto del movimento in atto e possiamo determinare la velocità del corpo e la sua posizione ad ogni istante. Il quadro che si ottiene è completo e conciso.

Ordini di grandezza

Nel mondo fisico convivono grandezze piccole insieme a grandezze molto grandi: le dimensioni di un atomo e le dimensioni dell’universo; il tempo che occorre alla luce per andare da questa pagina all’occhio di chi guarda e l’età dell’universo; la massa dell’elettrone e le masse galattiche.

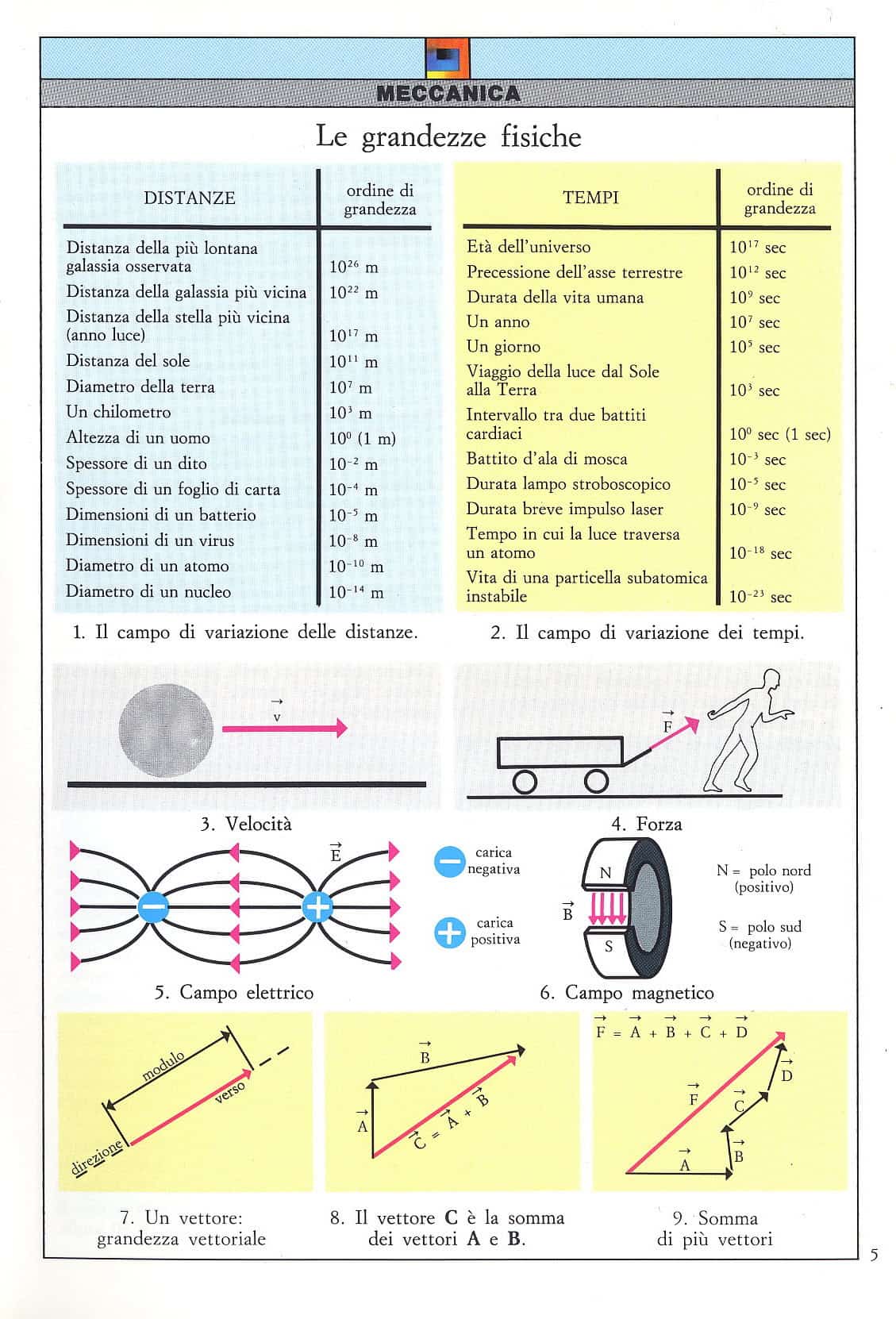
La distanza della più lontana galassia osservata è, ad esempio, cento milioni di milioni di milioni (→ 1) di volte l’altezza di un uomo, mentre l’esistenza di una particella subatomica instabile è un milionesimo di milioni di milioni di milioni (→ 1) la durata di un battito cardiaco.

Trattando di misure – per le distanze, i tempi e le masse -, nell’intervallo accessibile alla sperimentazione fisica, dovremo ricorrere a una notazione fondata sulle cosiddette potenze di 10.

Ad esempio: moltiplicando 10 per se stesso un certo numero di volte, si ha: 10 x 10 = 100 = 10², 10 x 10 x 10 = 1000 = 10³ …: il numero di volte, per cui 10 è moltiplicato per se stesso, figura nel risultato quale esponente di 10. Quando la potenza di 10 è presente nel denominatore, si attribuisce all’esponente il segno negativo: 1/10 = 0,1 = 10^-1, 1/100 = 0,01=10^-2 … Una potenza di 10 si dice ordine di grandezza.

La figura (→ 1) indica, in forma schematica, lo straordinario campo di variazione delle distanze presenti nell’universo: un intervallo superiore – come si può vedere, ai quaranta ordini di grandezza.

La figura successiva (→ 2) riporta invece gli ordini di grandezza riferiti ai tempi

Grandezze scalari e grandezze vettoriali

Sono grandezze scalari il volume, la massa, la temperatura, il tempo, l’energia, ecc., grandezze definite mediante il semplice numero che ne dà la misura di valore rispetto a una determinata scala di riferimento (di volumi, di masse, di scienza, che il corpo parte da uno stato di temperatura, ecc.).

Altre grandezze, definite non con un semplice numero ma con numeri associati a simboli di direzione e verso, prendono il nome di grandezze vettoriali. Non basta dire che un’auto ha percorso 10 km, ma occorre precisare la direzione e il verso del movimento.

Sono esempi tipici di grandezze vettoriali: lo spostamento di un corpo, la sua velocità (→ 3), l’accelerazione, la forza (→ 4); un campo elettrico (→ 5); un campo magnetico (→ 6).

Tutte queste grandezze sono rappresentate da vettori (→ 7), cioè da segmenti, orientati da una freccia, che ne determina la direzione e il verso. La lunghezza (modulo) del vettore, determinata rispetto all’unità prefissata, ne misura l’intensità.

Due vettori si dicono uguali quando hanno moduli identici e direzione e verso uguali. I vettori si possono rappresentare con i simboli in grassetto: a, b, c…

Per sommare i vettori A e B, si fa coincidere l’origine di A con l’estremità di B, ottenendo così il vettore-somma C = A + B (→ 8).

La regola vale per qualunque numero di vettori; si può inoltre dimostrare che, quale che sia l’ordine dei vettori (proprietà commutativa), si ottiene sempre lo stesso vettore-somma.